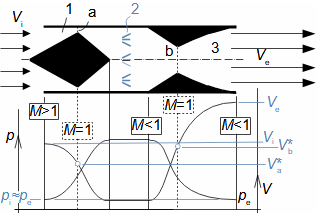
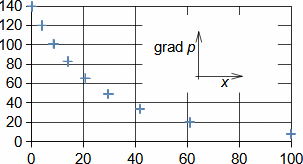
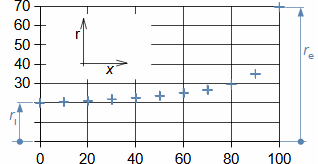
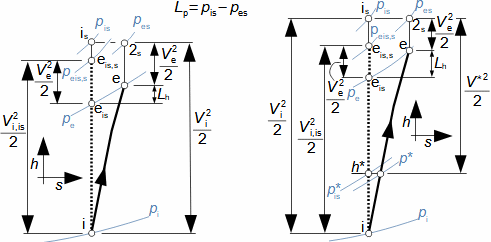
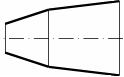
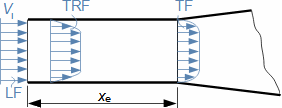
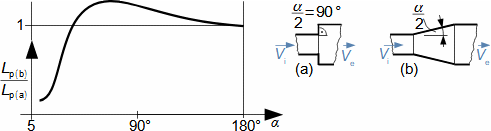
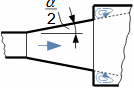
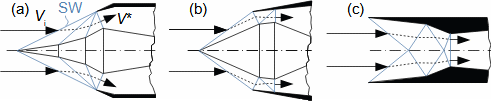
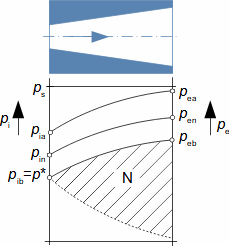
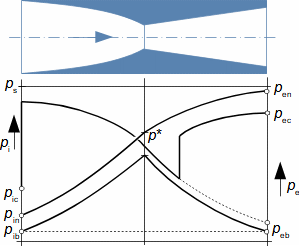
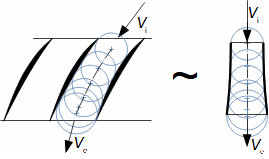
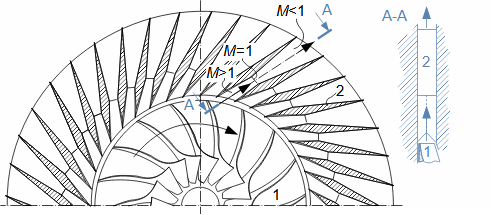
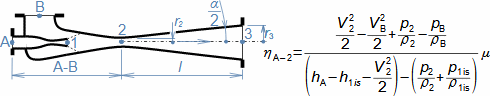Proudění plynů a par difuzory

Klíčová slovaPROUDĚNÍ PLYNŮ A PAR DIFUZORY

5.3

Co jsou difuzory a další využití teorie difuzorů

Nadzvukový difuzor

Podzvukový difuzor

Difuzor je kanál s plynulou změnou průtočného průřezu. Proudění tekutiny v difuzoru je děj, při kterém dochází především ke zvýšení tlaku a snížení kinetické energie. Podle Hugoniotovy věty vyhovuje nadzvukové vstupní rychlosti jiný tvar difuzoru než pro podzvukové vstupní rychlosti. V případě nadzvukové vstupní rychlosti musí nejdříve dojít ke zpomalení proudění na rychlost zvuku ve zužující se části difuzoru, viz Obrázek 1.

1: Dva základní typy difuzorů

vlevo-difuzor pro podzvukové rychlosti; vpravo-difuzor pro nadzvukové rychlosti. A [m²] průtočný průřez difuzoru; V [m·s^-1] rychlost plynu; M [Mach] Machovo číslo; A* [m²] kritický průřez nadzvukového difuzoru, ve kterém plyn dosahuje právě rychlosti zvuku neboli kritického stavu. Index _i označuje stav na vstupu do difuzoru, index _e označuje stav na výstupu z difuzoru.

Difuzorový kanál

Teorie difuzorů má široké uplatnění v různých typech proudových strojů s difuzorovými tvary kanálů. Pomocí propracované teorie difuzorů lze totiž popsat i, na první pohled, velmi složité proudění, na víc je k dispozici velké množství naměřených dat pro různé tvary difuzorů.

Energetická rovnováha difuzorů

Energetická rovnováha difuzorů vychází z prvního zákona termodynamiky a jejím základním výsledkem je účinnost diffuzoru. Často se používá i pojem hydraulická účinnost difuzoru, jestliže jsou změny hustoty uvnitř difuzoru nevýznamné.

Účinnost

Ztráty v difuzoru

Izoentropická komprese

Tlaková ztráta

h-s diagram

Kompresi v difuzoru ovlivňuje disipace energie, respektive ztráty. K identifikaci skutečných stavů plynu při průtoku difuzorem a ztrát lze použít h-s diagram, přičemž porovnávacím (ideálním) dějem je izoentropická komprese se stejným tlakem na výstupu a rychlostí jako při skutečné kompresi, viz Obrázek 2. Tlaková ztráta L_p je pak definována jako ztráta mezi celkovým tlakem na výstupu a vstupu difuzoru. K překonání ztrát L_h a dosažení stejného tlaku jako při kompresi beze ztrát je nutné zvýšit kinetickou energii na vstupu do difuzor právě o hodnotu L_h.

Klíčová slovaPROUDĚNÍ PLYNŮ A PAR DIFUZORY

5.4

2: Změna stavových veličin plynu v difuzoru

vlevo-diagram h-s podzvukového difuzoru; vpravo-diagram h-s nadzvukového difuzoru. h [J·kg^-1] entalpie plynu; h* [J·kg^-1] kritická entalpie; p [Pa] tlak plynu; s [J·kg^-1·K^-1] entropie; t [°C] teplota plynu; V* [m·s^-1] kritická rychlost; L_h [J·kg^-1] ztráta v difuzoru; L_p [Pa] tlaková ztráta. Index _s označuje celkový stav plynu, index _is izoentropickou kompresi.

Hmotnostní tok

Hmotnostní tok plynu difuzorem závisí na velikosti nejmenšího průřezu difuzoru, což je u podzvukového vstupní průřez A_i a u nadzvukového kritický průřez difuzoru A*. Hmotnostní tok se pak vypočítá z rovnice kontinuity pro parametry plynu v tomto průřezu.

Kritická rychlost

Kritická rychlost V* při reálné kompresi je stejná jako při izoentropické kompresi, protože rychlost zvuku v ideálním plynu je funkcí pouze teploty a izotermy odpovídají izoentalpám v h-s diagramu. To znamená, že přechod z nadzvukového do podzvukového proudění při reálné kompresi nastane při nižším tlaku než při izoentropické kompresi p*<p*_is. To je způsobeno nižší rychlostí plynu při stěnách difuzoru než v jádru proudu, proto střední rychlost plynu může být zvuková už při tlaku p*, zatím co v jádru proudu je ještě nadzvuková. Výše zmíněné skutečnosti znamenají, že plyn dosahuje kritické rychlosti – myšleno střední rychlost proudění – už před nejužším místem difuzoru.

Účinnost

Účinnost difuzoru může být definována různě. Nejčastěji se jedná o poměr mezi rozdílem entalpií při izoentropické a reálné kompresi, protože se tyto stavy nejsnáze zjišťují, viz Vzorec 3.

3: Účinnost difuzoru

η [1] účinnost difuzoru definována ke statickým stavům plynu (účinnost stanovená k celkovým stavům entalpie bude mít vyšší hodnotu, což je patrné z h-s diagramu).

Klíčová slovaPROUDĚNÍ PLYNŮ A PAR DIFUZORY

5.5

Podobné difuzory při podobných provozních podmínkách budou mít i podobné účinnosti. Tuto podobnost lze využít při návrhu nového difuzoru při predikci jeho parametrů na základě odhadu jeho účinnosti. Přesnost takového návrhu je závislá na míře podobnosti porovnávaných difuzorů.

Hydraulická účinnost

V případě kapalin, nebo nevýznamné změně hustoty plynu, se vychází při energetické bilanci difuzoru z Bernoulliho rovnice. V difuzoru kapalina nekoná vnější práci, takže celková energie kapaliny před difuzorem musí být rovna celkové energie kapaliny na výstupu z difuzoru s připočtením ztrát, viz Vzorec 4.

4: Energetická rovnováha difuzoru při proudění kapaliny

g [m·s^-2] gravitační zrychlení; H_{i, e} [J·kg^-1] celková energie kapaliny na vstupu, respektive výstupu; z [m] výška osy difuzoru od referenční roviny; ρ [kg·m^-3] hustota.

V těchto případech lze účinnost difuzoru, označovaná jako hydraulická, definovat jako podíl mezi celkovou energii kapaliny na výstupu a na vstupu difuzoru (Vzorec 5).

5: Hydraulická účinnost difuzoru

Tvary difuzorů

V praxi se používají v podstatě jen dva tvary difuzorů. Nejjednodušším tvarem je kuželový difuzor s konstantním úhlem rozšíření difuzoru. Ostatní difuzory označované jako kornoutové mají úhel rozšíření difuzoru proměnlivý podle požadavku na gradient tlaku v difuzoru.

Gradient tlaku

Vlastnosti difuzorů velmi závisejí na rozložení gradientu tlaku v difuzoru, který lze stanovit pro případ proudění beze ztrát a ideální plyn pomocí Rovnice 6. V případě reálných dějů lze gradinet tlaku vypočítat pomocí termodynamických dat reálných plynů, viz Úloha 2.

Klíčová slovaPROUDĚNÍ PLYNŮ A PAR DIFUZORY

5.6

6: Gradient tlaku v difuzoru

κ [1] konstanta adiabatického děje (poměr tepelných kapacit). Tato rovnice je odvozena za zjednodušujícího předpokladu, že rychlost proudění má v celém průřezu pouze osový směr a pro ideální plyn. Odvození je uvedeno v Příloze 4.

Kuželové difuzory

Úhel rozšíření difuzoru

Kuželový tvar difuzoru (Obrázek 7) se jednoduše vyrábí a to i v případě nekruhových variant. Podle [Dejč, 1967, s. 391] se úhel rozšíření α pohybuje v rozmezí 6 až 15°, přičemž většina difuzorů se vyrábí s úhlem rozšíření ve středním rozsahu 10 až 12°.

7: Kuželový difuzor

r [m] poloměr; α [°] úhel rozšíření difuzoru; l [m] délka difuzoru; x [m] vzdálenost na ose.

Odtržení proudu

Nevýhodou kuželových difuzorů je velmi rychlý pokles tlaku u vstupu do difuzoru, takže ke konci difuzoru už je velmi malý gradient tlaku (viz Úloha 1), respektive velmi nízká energie proudu. To způsobuje zvýšenou míru pravděpodobnosti odtržení proudu od stěn difuzoru.

Kornoutové difuzory

Gradient tlaku

Kuželové difuzory

Difuzory s proměným úhlem rozšíření α se nazývají kornoutové a jsou navržené pro požadovaný gradient tlaku. Nejčastěji jsou kornoutové difuzory navrženy na konstantní gradient tlaku (Obrázek 8a) nebo jeho linerání pokles (Obrázek 8b). Kornoutové difuzory mají na konci prudké rozšíření (viz Úloha 2), proto lze očekávat, že jsou citlivější na odtržení mezní vrstvy od stěny než difuzory kuželové. Měření ukazují, že tomu tak je u dlouhých difuzorů, ale u krátkých difuzorů (kuželové difuzory s α>18°) je tomu naopak [Dejč, 1967, s. 392].

Klíčová slovaPROUDĚNÍ PLYNŮ A PAR DIFUZORY

5.7

8: Kornoutové difuzory

(a) difuzor s konstantním gradientem tlaku, viz jeho výpočet v Úloze 2; (b) difuzor s lineárním poklesem gradientu tlaku.

Konstatní gradient tlaku

Rychlostní profil

Tepelný výměník

Difuzory s konstantním gradientem tlaku mají také rovnoměrnější rychlostní profil než difuzory kuželové a proto se také používají před chladiči, respektive tepelnými výměníky s požadavkem na rovnoměrné rozložení hmotnostního toku po průtočné ploše výměníku [Goroščenko, 1952, s. 67], [Frass, 1989, s. 155].

Lineární gradient tlaku

Odtržení proudu

V difuzoru navržený na linerání pokles gradientu tlaku (Obrázek 8b) se gradient tlaku snižuje postupně, tak jak klesá energie v mezní vrstvě (přibližně lineárně), a proto je to tvar s nejmenší pravděpodobností odtržení proudu [Dejč, 1967, s. 388].

Plynulé změny tvaru difuzorů s proměným úhlem rozšíření difuzoru jsou výrobně složité a proto se nahrazují kombinací dvou a více více kuželových dufuzorů s různými uhly rozšířen, viz Obrázek 9, [Dejč, 1967, s. 393].

9: Praktické řešení difuzorů s proměnným rozšířením

Odtržení proudu

Vnitřní tření

Rychlostní profil

V difuzorech vznikají ztráty způsobené vnitřním třením, případně rázovými vlnami a ztrátou vzniklou při odtržení mezní vrstvy od stěn difuzoru. Průběh odtržení mezní vrstvy od stěny je zobrazen na Obrázku 10. K odtržení mezní vrstvy dochází v důsledku poklesu celkového tlaku v mezní vrstvě pod statický tlak za difuzorem. V takovém okamžiku dojde ke zpětnému proudění pracovní tekutiny podél stěny difuzoru a k odtržení mezní vrstvy od stěny. Celkový tlak klesá v mezní vrstvě kvůli ztrátě kinetické energie proudu. Ztráta vzniklá odtržením mezní vrstvy se projeví na nárůstu tlakové ztráty difuzoru.

Klíčová slovaPROUDĚNÍ PLYNŮ A PAR DIFUZORY

5.8

10: Mechanismus odtržení mezní vrstvy od stěny difuzoru a následný vznik vírů

VP-rychlostní profil (velocity profile).

Turbulence

Turbulizátor

Hrdlo

Ztráta při odtržení proudu je tím větší, čím dále od konce difuzoru k odtržení dojde. Polohu odtržení lze ovlivnit například zvýšením turbulencí v difuzoru, protože při nich dochází ke sdílení energie a hybnosti jádra proudu s mezní vrstvou, tento jev u laminárního proudění chybí. Je-li žádoucí dosáhnout turbulentního proudění, potom je nutné zajistit již na vstupu do difuzoru plně vyvinuté proudění. Toho se nejčastěji dosahuje přidáním turbulizátoru nebo hrdla před difuzor, ve kterém proběhne vývoj mezní vrstvy až do turbulence, viz Obrázek 11.

11: Vývoj rychlostního profilu v hrdle difuzoru

LF-oblast laminárního proudění (laminar flow); TRF-přechodová oblast (transition flow); TP-plně vyvinuté turbulentní proudění (turbulent flow). x_e [m] minimální délka hrdla difuzoru pro úplný vývoj mezní vrstvy.

Sací trouba

Obvodová rychlost

Přisávání

Mezní vrstvu lze také stabilizovat pomocí obvodové složky rychlosti a odstředivá síla způsobí vyšší tlak u stěn difuzoru. Typickým příkladem jsou sací trouby vodních turbín, ve kterých se využívá pro stabilizaci mezní vrstvy malá obvodová složka proudění na výstupu z turbíny. Proudění na konci difuzoru lze také stabilizovat přisáváním plynu přes otvory ve stěnách difuzoru apod (viz [Japikse and Baines, 1995]).

Tlaková ztráta

Odtržení proudu se projeví i na velikosti tlakové ztráty L_p difuzoru (definice viz Rovnice 2). Tlaková ztráta je také funkcí délky difuzoru a úhlu rozšíření. Při posuzování vlivu těchto parametrů na tlakovou ztrátu L_p v difuzoru se používá porovnání s náhle rozšířeným kanálem stejných průtočných průřezů, viz Obrázek 12. Tak lze vyhodnotit, kdy má smysl konstruovat difzor s úhlem rozšíření a kdy postačí náhlé rozšíření.

Klíčová slovaPROUDĚNÍ PLYNŮ A PAR DIFUZORY

5.9

12: Vliv rozšíření kuželového difuzoru na tlakovou ztrátu

Graf v měřítku je uveden v [Dejč, 1967, s. 382].

Škrcení

Podle Obrázku 12 může být tlaková ztráta kuželového difuzoru od určitého úhlu větší než pro případ náhle rozšířeného kanálu. To je způsobeno tím, že ztráta vnitřním třením klesá s úhlem rozšíření α, ale ztráta vířením při odtržení mezní vrstvy s úhlem α roste. Takže při proudění náhle rozšířeným průřezem vznikají pouze víry při odtržení [Maštovský, 1964, s. 88], které způsobují zvýšení entropie stejným mechanismem jako při škrcení proudu clonou.

Krátké difuzory

Jestliže je nutné difuzor zkrátit, pak je výhodnější použít kombinaci uvedenou na Obrázku 13, než zvětšit úhel rozšíření difuzoru. Toto řešení lze přirovnat k hladkému kornoutovému difuzoru na Obrázku 8a.

Praktická řešení prostorově omezených difuzorů

13: Praktické řešení prostorově omezeného difuzoru

Nadzvukové difuzory

Metoda charakteristik

Šikmé rázové vlny

Návrh nadzvukového difuzoru je problematický. V ideálním případě by měla komprese v difuzoru probíhat skrz kompresní vlny, které jsou opakem vln expanzních. Kompresní vlny by měly vznikat v konvergentní části difuzoru, která odpovídá obrácené ideální Lavalově trysce navržené metodou charaketeristik. Takové nadzvukové difuzory se ale nevyrábí, protože při reálném proudění vzniknou šikmé rázové vlny už na vstupních hranách difuzoru a další uvnitř konvergentní části [Dejč, 1967, s. 405].

Klíčová slovaPROUDĚNÍ PLYNŮ A PAR DIFUZORY

5.10

Stupňovité difuzory

Nadzvukový let

Nejlepší stability proudění dosahují v reálných podmínkách takové nadzvukové difuzory, které mají stupňovité zbrzdění proudu (Obrázek 14). Ty jsou tvarovány tak, aby v určitých místech vznikaly na sebe navazující šikmé rázové vlny s postupně větším sklonem, takže poslední vlna v nejužším místě difuzoru je kolmá. Nadzvukové stupňovité difuzory se snadno navrhují, protože chování šikmých rázových vln je dobře probádáno a popsáno. V těchto případech se tedy vždy počítá i se ztrátami, které rázové vlny mohou způsobit. Difuzory na Obrázku 14 jsou difuzory proudových motorů a zajišťují, že do motoru bude vstupovat podzvukové proudění i při nadzvukovém letu.

14: Nadzvukové difuzory se stupňovitým zbrzděním proudu

(a) stupňovitý nadzvukový difuzor; (b), (c) stupňovitý nadzvukový difuzor s navazujícími rázovými vlnami – jako by se odrážely od stěny difuzoru – což přirozeně usměrňuje vektor rychlosti do osového směru a snižuje ztráty [Dejč, 1967, s. 409]. SW-rázové vlny (shock waves).

Nenávrhové stavy difuzorů

Každý difuzor je navržen na konkrétní stav plynu před a za difuzorem. Jestliže se tento stav změní, změní se i proudění v difuzoru. Takový stav se nazývá nenávrhový. Při nenávrhových stavech se snižuje účinnost difuzoru (zejména při nižších průtocích roste ztráta odtržením mezní vrstvy od stěn) a může se i stát, že se difuzor změní na Lavalovu trysku.

Podzvukový difuzor

Ventil s difuzorem

Na Obrázku 15 jsou znázorněny dva nenávrhové stavy podzvukového difuzoru označené písmeny a, b (index n označuje návrhový stav). Tyto nenávrhové stavy jsou vyvolány změnou vstupní rychlosti V_i při stejném vstupním celkovém tlaku, přičemž platí: V_ia<V_in<V_ib=a. Rychlost V_ib je tedy zvuková, respektive kritická. U jednotlivých případů se mění i protitlak, kdyby byl stále stejný (p_e=p_en), tak by nemohla nastat rovnováha proudění. Pokud chceme udržovat protitlak, pak je nutné použít regulaci vstupního průtočného průřezu–takovou typickou aplikací je ventil s difuzorem. Při menším jak kritickém tlaku p* vzniká za nejužším průřezem rázová vlna a navíc při klesajícím protitlaku pod p_ec se stává z difuzoru Lavalova tryska, viz Hugoniotova věta.

Klíčová slovaPROUDĚNÍ PLYNŮ A PAR DIFUZORY

5.11

15: Vliv změny vstupní rychlosti na funkci podzvukového difuzoru

N-oblast funkce nadzvukové trysky (nozzle).

Nadzvukový difuzor

Lavalova tryska

Na Obrázku 16 jsou znázorněny dva nenávrhové stavy nadzvukového difuzoru označené písmeny a, b (index n označuje návrhový stav), přičemž platí V_ia<V_in<V_ib>a. U jednotlivých případů se mění i protitlak tak, aby podzvukové části difuzoru nevznikla rázová vlna. V případě varianty-a není konvergentní část difuzoru schopna pojmout takové množství plynu (bude klást velký odpor), proto ještě před difuzorem vznikne kolmá rázová vlna, která zvýší tlak na nadkritický a rychlost sníží na podzvukovou. Tím konvergentní část difuzoru bude fungovat jako tryska. Divergentní část difuzoru bude fungovat jako Lavalova tryska při nenávrhovém stavu.

16: Vliv změny vstupní rychlosti na funkci nadzvukového difuzoru

Klíčová slovaPROUDĚNÍ PLYNŮ A PAR DIFUZORY

5.12

Nadzvukový difuzor

Hrdlo

Možnost změny protitlaku nebo regulaci průtočného průřezu je podmínkou pro fungování nadzvukového difuzoru v širokém rozsahu vstupních parametrů. Mechanismus k regulaci kritického průřezu se nepoužívá do vstupní rychlosti cca M<1,5 Mach – před rozšiřující se části takového difuzoru je pouze hrdlo difuzoru s konstantním průřezem podobně, jak je zobrazeno na Obrázku 12. U této konstrukce se předpokládá, že na vstupu do hrdla vznikne kolmá rázová vlna [Dejč, 1967, s. 406], ve které se sníží rychlost na podzvukovou. Ztráty v takovém hrdle nebudou, při těchto rychlostech, ještě výrazné. Náročnější experimenty s proměnným protitlakem difuzorů, při kterých jsou záměrně vytvářeny rázové vlny, jsou uvedeny v [Dejč, 1967, s. 410-415].

Difuzorové profilové mříže

Kornoutový difuzor

Příčný tlakový gradient

Z Obrázku 17 je patrné, že difuzorové profilové mříže budou mít podobné vlastnosti jako kornoutové difuzory. Nicméně převod tvaru difuzorové profilové mříže na ekvivalentní symetrický difuzor je problematický. Jednoduchý geometrický převod z Obrázku 17 nemusí být, z pohledu proudových vlastností, vždy dostatečně vypovídající. Navíc citlivost na odtržení mezní vrstvy zvyšuje i příčný gradient tlaku, který v zahnutých kanále vzniká, proto jsou profily v difuzorových mříží málo zahnuté.

17: Geometrická podobnost difuzorové lopatkové mříže se symetrickým difuzorem

λ-rázová vlna

Jestliže nátoková rychlost na vstupu do difuzorové profilové mříže dosáhne nebo přesáhne kritické Machovo číslo, potom proudění přesáhne na sací straně profilu rychlost zvuku. Nicméně na výstupu z difuzorového kanálu je tlak vyšší než na vstupu a to i průtočný průřez, takže podle Hugoniotovy věty musí dojít ke skokové změně nadzvukové rychlosti na podzvukovou, to se děje lokálně blízko profilu v λ-rázové vlně, viz Obrázek 18. Opatření pro snížení vlivu takové rázové vlny je popsáno v [Kadrnožka, 2004, s. 136].

Klíčová slovaPROUDĚNÍ PLYNŮ A PAR DIFUZORY

5.13

18: Vznik λ-rázové vlny v profilové mříži kompresoru

Nadzvukový turbokompresor

Nadzvukové profilové mříže se používají jen výjimečně pro svou nízkou účinnost a špatnou regulovatelnost. Jejich použití je opodstatněné například u jednostupňových kompresorů s velmi vysokým kompresním poměrem, viz Obrázek 19.

19: Příklad uspořádání nadzvukového turbokompresoru

1-oběžné kolo radiálního kompresoru; 2-lopatky difuzoru se supersonickým profilem.

Ejektory a injektory

Proudový stroj

Ejektory a injektory jsou proudové stroje, které se využívají jako vývěvy, nebo čerpadla. Funkce ejektorů či injektorů je založena na předávání části kinetické energie hnací tekutiny tekutině hnané. To se děje přibližně v hrdle difuzoru, viz Obrázek 20, kde dochází k přisávání hnané tekutiny do paprsku tekutiny hnací. V difuzorové části stroje dochází k transformaci kinetické energie na energii tlakovou.

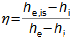
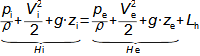
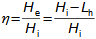
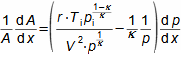
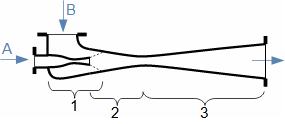
20: Obecné schéma ejektoru nebo injektoru

A-hnací tekutina; B-hnaná tekutina; 1-sací zóna; 2-hrdlo difuzoru (směšovací zóna); 3-výstupní difuzor.

Klíčová slovaPROUDĚNÍ PLYNŮ A PAR DIFUZORY

5.14

Ejektor vs. injektor

Rozdíl mezi ejektorem a injektorem je v tom, že na výstupu z ejektoru je tlak nižší než tlak hnací tekutiny na vstupu. Na výstupu z injektoru je naopak tlak vyšší než tlak hnací tekutiny.

Hrdlo

Tlak ve směšovací zóně

Tvar hrdla difuzoru musí být navržen tak, aby v něm docházelo k postupnému předávání kinetické energie hnané tekutině a vyrovnání rychlostního pole. V hrdle difuzoru už musí také docházet k transformaci kinetické energie na tlakovou, to přispívá ke stabilizaci rychlostního pole a současně snižuje vnitřním tření v difuzoru, jenž je funkcí rychlosti proudění. Takže tlak na vstupu do difuzorové části bude větší než tlak na sání hnané tekutiny.

Ejekční poměr

Poměr mezi hmotnostním tokem hnané a hnací tekutiny, označovaný jako ejekční poměr, lze stanovit z energetické bilance směšování v hrdle difuzoru, viz Vzorec 21.

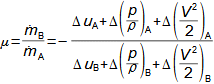
21: Energetická rovnováha ejektorů a injektorů

u [J·kg^-1] vnitřní tepelná energie 1 kg pracovní tekutiny; μ [1] ejekční poměr [Dejč, 1967, s. 419]. Odvození rovnice při vynechání vlivu změny potenciální energie je v Příloze 5. Výpočet ejektoru a injektoru je také proveden v [Hibš, 1981], [Dejč, 1967], [Kadrnožka, 1984], [Nechleba and Hušek, 1966].

Vnitřní tepelná energie

Vnitřní tepelná energie v proudovém čerpadle se zvyšuje v důsledku ztrát (transformace kinetické energie nebo tlakové na tepelnou) nebo sdílením tepla hnací a hnané tekutiny. K největší změně vnitřní tepelné energie dochází, jestliže jedna z pracovních tekutin kondenzuje v prostoru hrdla. Typickým příkladem je proudové čerpadlo parního kotle, viz Úloha 3.

Ejektory

Těžební čerpadlo

Vývěva

Ejektory mají široké uplatnění v průmyslu, v důlním průmyslu se používají pro čerpání kapalin s velkých hloubek [Nechleba and Hušek, 1966, s. 218], v energetice pro odsávaní parovzdušné směsi z kondenzátoru parních turbín, kde hnací tekutinou je pára (Obrázek 22).

Příklad provedení parního ejektoru ve funkci jako vývěvy parního kondenzátoru [Nožička, 2000]

22: Příklad provedení parního ejektoru jako vývěvy parního kondenzátoru [Nožička, 2000]

Klíčová slovaPROUDĚNÍ PLYNŮ A PAR DIFUZORY

5.15

Injektory

Proudové čerpadlo

Injektory se používají jako napájecí čerpadla vody do parních kotlů parních lokomotiv. Proudovým čerpadlem parního kotle je voda čerpána do vyššího tlaku pomocí páry, která má na vstupu tlak nižší, než je výstupní tlak difuzoru p_e. To je možné díky velmi vysoké kinetické energie páry, kterou může pára v trysce získat při expanzi, viz Úloha 3. Pára tuto kinetickou energii ve směšovací komoře předává vodě a současně kondenzuje. Nutnou podmínkou funkce takového čerpadla je, aby pára zkondenzovala ještě v hrdle difuzoru, respektive aby difuzorem protékala jen kapalina bez bublinek páry, jinak nelze dosáhnout požadovaného tlaku. Navíc bublinky páry zvyšují riziko kavitačního opotřebení difuzoru. Hnací pára zcela zkondenzuje v hrdle difuzoru, pokud přisává odpovídající množství studené vody (hnaná kapalina). To znamná, že s teplotou nasávané vody (hnané tekutiny), klesá výkon čerpadla.

Náporové motory

Náporové motory využívají ke kompresi vzduchu nadzvukový difuzor v ústí motoru při nadzvukovém letu. Stlačený vzduch je následně spalován ve spalovací komoře s palivem a horké spaliny expandují v trysce a vytváří tah. Oproti turbokompresorovým motorům neobsahují turbokompresorovou a turbínovou část. Při pohybu nadzvukovou rychlostí se významně mění hodnoty dosažených tlaků, odtud rozlišujeme konstrukci náporového motoru typu Ramjet vhodný pro nižší nadzvukové rychlosti a typu Scramjet vhodnější pro velmi vysoké nadzvukové rychlosti.

Ramjet

Na Obrázku 23 je funkce náporového motoru typu Ramjet, který je charakteristický dvěma kritickými průřezy a to pro vstup komprimovaného vzduchu a výstup horkých spalin. Hmotnostní průtok tryskou je vyšší než hmotnostní průtok vzduchu v kritickém průřezu difuzoru-b o množství paliva. Proto řízení výkonu takového motoru je obtížné (při poklesu průtoku klesá tlak ve spalovací komoře).

Klíčová slovaPROUDĚNÍ PLYNŮ A PAR DIFUZORY

5.16

23: Náporový motor typu ramjet

a-vstupní kritický průřez; b-výstupní kritický průřez. 1-nadzvukový difuzor; 2-spalovací komora a přívod paliva do podzvukového proudu; 3-expanze spalin v trysce.

Náporové motory samostatně pracují až při vyšších rychlostech (maximální účinnosti dosahují při 5 Maších). Například britská střela GWS-30 Sea Dart používá motor ramjet v kombinaci se startovacím raketovým motorem na tuhé palivo.

Scramjet

Pružnější regulaci výkonu náporového motoru lze získat sloučením kritického průřezu difuzoru a trysky – taková konstrukce motoru se nazývá scramjet, jehož schéma je uvedeno na Obrázku 24(a). Vstřik a hoření paliva probíhá přímo v kritickém průřezu. Tento náporový motor je schopen pracovat v mnohem širším rozsahu rychlostí než konstrukce ramjet, ale aby motor začal pracovat musí být rychlost letadla mnohem vyšší než rychlost zvuku. Maximální účinnosti dosahují motory Scramjet až při 9 Maších.

24: Náporový motor Scramjet

(a) schéma funkce motoru; (b) experimentální bezpilotní letoun X-43A s pohonem Scramjet. 1-nadzvukový difuzor; 2-spalovací komora v nejužším místě motoru a přívod paliva do zvukového proudu; 3-expanze spalin v trysce; 4-systém rázových vln; 5-nástavby na vstřik paliva do nadzvukového proudu; 6-expanzní vlny.

Klíčová slovaPROUDĚNÍ PLYNŮ A PAR DIFUZORY

5.17

Experimentální bezpilotního letoun X-43A s pohonem Scramjet dosáhl rychlosti 6,83 Machů během 10 minutového letu. Pracovní rychlosti dosáhl pomocí urychlovací rakety ve výšce 30 000 m, přičemž celá soustava byla vypuštěna z bombardéru B-52B. Letoun X-43A využívá efektu šikmo seříznuté Lavalovy trysky, tj. vytvoření expanzních vln, které nahrazují protilehlou stěnu trysky – letoun je tím lehčí.

Úlohy

Úloha 1:

Vypočítejte úhel rozšíření kuželového difuzoru a stanovte průběh gradientu tlaku v tomto difuzoru, jestliže jeho délka je 100 mm a počátečního poloměru 20 mm. Parametry na vstupu do difuzoru: 82 m·s^-1, 110 kPa, 20 °C, suchý vzduch. Parametry na výstupu: 114 kPa. Uvažujte proudění beze ztrát. Řešení úlohy je uvedeno v Příloze 1.

grad p [kPa·m^-1] gradient tlaku; x [mm].

§1:

zadání:

l; r_i; V_i; p_i; t_i; p_e

§3:

výpočet:

v_i; v_e; A_i; ε_e; V_e; A_e; r_e; α

§2:

odečet:

r; κ

§4:

výpočet:

grad p

Popisek symbolů je uveden v Příloze 1.

Úloha 2:

Kournoutový difuzor

Navrhněte kornoutový difuzor kruhového průřezu odpovídající požadavku dp/dx=konst. Parametry na vstupu do difuzoru: 82 m·s^-1, 110 kPa, 20 °C, suchý vzduch. Parametry na výstupu: 114 kPa. Požadovaná délka difuzoru je 100 mm při vstupním poloměru 20 mm. Uvažujte účinnost difuzoru 93 % s rovnoměrně rozloženými ztrátami. Řešení úlohy je uvedeno v Příloze 2.

Vypočítaný průběh poloměru difuzoru s konstantním tlakovým gradientem – tzv. kornoutový tvar [Frass, 1989, s. 156]. r [mm]; x [mm]

Klíčová slovaPROUDĚNÍ PLYNŮ A PAR DIFUZORY

5.18

§1:

zadání:

V_i; p_i; t_i; p_e; l; r_i; η

§3:

odečet:

stavy vzduchu pro jednotlivé p_x z h-s

§2:

výpočet:

p_x pro jednotlivé souřadnice x

§4:

výpočet:

r_x pro jednotlivé x

Popisek symbolů je uveden v Příloze 2.

Úloha 3:

Navrhněte základní rozměry injektoru (proudového napájecího čerpadla) parního kotle (injektor). Napájecí voda je čerpána z otevřené nádrže o teplotě 70 °C do tlaku 0,54 MPa. Požadovaný průtok napájecí vody je 60 kg·h^-1. Účinnost difuzorové části uvažujete 80 %. Hodnota účinnosti trysky zahrnuje i účinnost předávání kinetické energie z páry čerpané vodě a činí 10 %. Rychlost syté páry na vstupu do čerpadla je 20 m·s^-1. Rychlost vody na vstupu i výstupu čerpadla je 3 m·s^-1. Neuvažujte tlakové ztráty v kotli a v potrubí. Řešení úlohy je uvedeno v Příloze 3.

η_A-2 [1] účinnost expanze v trysce a předávání hybnosti ve směšovací komoře (odvození v Příloze 3, §4).

§1:

zadání:

p_B; t_B; p₃; m_B; η_2-3; η_A-2; V_A;
V₃; V_B

§5:

odečet:

ρ3

§2:

odečet:

h_A; s_A; h_B; ρ_B; p_1is; h_1is; ρ_1is

§6:

porovnání:

ρ3 §5 vs. ρ3 §3

§3:

odhad:

ρ3

§7:

návrh:

V₂; α

§4:

výpočet:

μ; h₃

§8:

výpočet:

m; A₃; A₂; r₃; r₂; l

Popisek symbolů je uveden v Příloze 3.

Odkazy

ŠKORPÍK, Jiří, 2023, Technická matematika, engineering-sciences.education, Brno, engineering-sciences.education/technicka-matematika.html.

ŠKORPÍK, Jiří, 2024, Technická termomechanika, engineering-sciences.education, Brno, [on-line], ISSN 1804-8293. Dostupné z https://engineering-sciences.education/technicka-termomechanika.html.

DEJČ, Michail, 1967, Technická dynamika plynů, SNTL, Praha.

FRAAS, Arthur, 1989, Heat exchanger design, John Wiley&Sons, Inc., ISBN 0-471-62868-9.

GOROŠČENKO, B. T., 1952, Aerodynamika rychlých letounů, Technicko-vědecké vydavatelství, Praha.

HIBŠ, Miroslav, 1981, Proudové přístroje, SNTL – Nakladatelství technické literatury, n. p., Praha, DT 621.694.

JAPIKSE, David, BAINES, N., 1995, Diffuser design technology, Concepts ETI, Norwich, ISBN 0933283083.

KADRNOŽKA, Jaroslav, 1984, Tepelné elektrárny a teplárny, SNTL-Nakladatelství technické literatury, Praha.

KADRNOŽKA, Jaroslav, 2004, Tepelné turbíny a turbokompresory I, Akademické nakladatelství CERM, s.r.o., Brno, ISBN 80-7204-346-3.

MAŠTOVSKÝ, Otakar, 1964, Hydromechanika, Statní nakladatelství technické literatury, Praha.

MICHELE, F. et al., 2010, Historie a současnost Parní turbíny v Brně, Siemens, Brno, ISBN: 978-80-902681-3-5.

NECHLEBA, Miroslav, HUŠEK, Josef, 1966, Hydraulické stroje, Státní nakladatelství technické literatury, Praha.

NOŽIČKA, Jiří, 2000, Osudy a proměny trysky Lavalovy, Bulletin asociace strojních inženýrů, č. 23, ASI, Praha.

Doplňkový mediální obsah

Skvělou ukázkou stabilizace proudění u stěn difuzoru je zadní křídlo formulí/rear wing. To funguje jako difuzor a rozdělením jeho profilu do více umožňuje přisávat proudění pod křídlo, a tím stabilizovat mezní vrstvu,která je odolnější vůči odtržení/stall. https://t.co/qlDcJsIIn0 pic.twitter.com/ULrvy1Zeej
— Jiří Škorpík (@jiri_skorpik) February 7, 2023

Zmíněná nadzvuková střela s náporovým motorem GWS-30 Sea Dart právě startuje na obrázku vlevo pomocí urychlovacího raketového motor. Sací otvor se supersonickým difuzorem je dobře patrný na špici střely. https://t.co/TRFSgs6vcr
— Jiří Škorpík (@jiri_skorpik) February 10, 2023

U tohoto typu letounu dochází k hoření paliva v okolí trupu, který má tvar Lavalovy trysky. Oblast hoření a expanze je udržována díky rázovým vlnám. Více zde: https://t.co/bjjzuVlzvs https://t.co/5JhD7qzXB8
— Jiří Škorpík (@jiri_skorpik) November 17, 2022