MACHOVO ČÍSLO A EFEKTY PŘI PROUDĚNÍ VYSOKÝMI RYCHLOSTMI

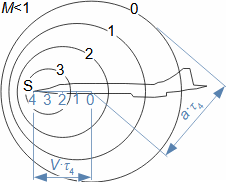
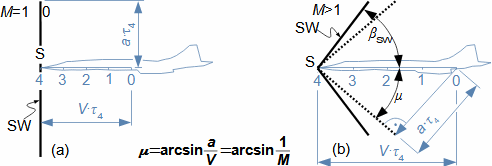
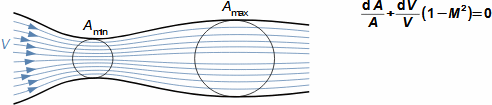
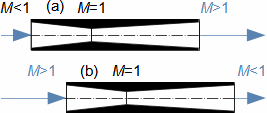
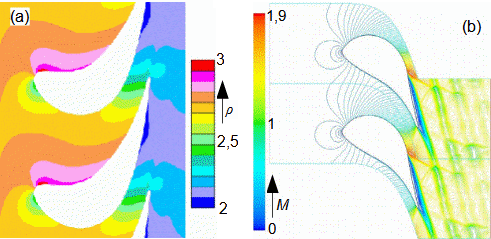
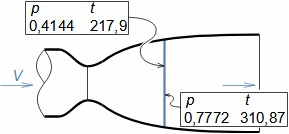
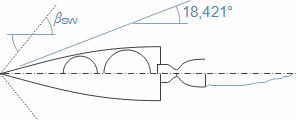
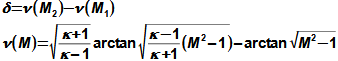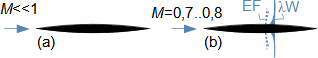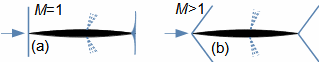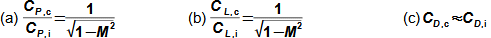Základní pojmy v proudění vysokými rychlostmi

Machovo číslo

Rychlost zvuku

Stlačitelná tekutina

Machovo číslo je definováno jako poměr rychlosti proudu ku rychlosti šíření zvuku v tekutině (Rovnice 1). Jestliže Machovo číslo dosáhne takové velikosti, při které už pro danou aplikaci nelze uvažovat tekutinu za nestlačitelnou, pak takovou rychlost označuje v aerodynamice za vysokou. Stlačitelnost totiž způsobuje efekty v proudění, které se při proudění nestlačitelných tekutin nebo nízkých Machových číslech nevyskytují.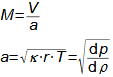

1: Definice Machova čísla a rychlosti zvuku

a [m·s^-1] rychlost šíření zvuku ve vyšetřovaném kontinuu; M [Mach] Machovo číslo; p [Pa] tlak; r [J·kg^-1·K^-1] individuální plynová konstanta; T [K] absolutní teplota plynu (statická teplota); V [m·s^-1] rychlost tělesa nebo proudění; ρ [kg·m^-3] hustota; κ [1] poměr tepelných kapacit. Odvození rovnice pro rychlost zvuku je v Příloze 3.

Podzvukové proudění

Transsonické proudění

Zvukové proudění

Nadzvukové proudění

Jestliže je v okolí vyšetřovaného bodu tekutiny Machovo číslo menší než jedna (M<1), pak mluvíme o podzvukovém (subsonických) proudění. Jestliže se v okolí vyšetřovaného bodu tekutiny pohybuje hodnota Machova čísla kolem 1, konkrétně v rozmezí 0,8<M<1,3, pak mluvíme o transsonickém proudění – speciálně při velikosti Machova čísla právě 1 (M=1) mluvíme o zvukovém (sonické) proudění. Jestliže se v celém okolí vyšetřovaného bodu tekutiny pohybuje hodnota Machova čísla nad hodnotu 1 (M>1), pak mluvíme o nadzvukovém (supsonickém) proudění.

Kritické Machovo číslo

Někdy se setkáme s pojmem kritické Machovo číslo, toto číslo je vztaženo k nějakému jasně definovanému bodu v rámci vyšetřovaného objemu tekutiny, a jedná se o takovou velikost Machova čísla, při které se někde v daném objemu dosáhne zvukové nebo nadzvukové rychlosti (například v důsledku obtékání nějakých těles uvnitř).

3: Šíření zvukových vln při pohybu zdroje tlakové poruchy

τ [s] čas. Kružnice 0, 1, 2, 3 představuji hranici zvukových vln v prostředí v čase τ=0...3. V čase 0 je zdroj právě na souřadnici 0 v čase 1 na souřadnici 1 atd. Tj. v bodě 0 vyvolá zdroj tlakovou poruchu, která se šíří rychlostí zvuku v kulové ploše, poté co urazí zdroj vzdálenost 0-S bude mít poloměr zvukové vlny označený na obrázku symbolem 0. Stejný postup platí i pro tlakovou poruchu vyvolanou zdrojem v bodě 1 atd.

Nadzvukové proudění

Tlaková porucha

Rázové vlny

Pokud rychlost zdroje tlakové poruchy ve stlačitelném prostředí je blízká rychlosti zvuku nebo je dokonce vyšší, potom dochází k efektům narušující spojitost stlačitelného prostředí (skokové změny stavových veličin) a místo šíření tlakové poruchy formou zvukových vln se šíří formou tzv. rázových vln.

Úhel rázové vlny

Machův úhel

V případě zvukových a nadzvukových rychlostí (M≥1) je čelo tlakových poruch neustále v místě zdroje. To způsobí, že proudnice se před obtékaným tělesem nerozestupují a toto těleso je nuceno svým objemem okolní plyn vytěsnit prudkou kompresí – energie ke kompresi plynu v rázové vlně je brána z pohybu tělesa. Takto zkomprimovaný plyn postupně expanduje směrem od tělesa. Hranici komprimovaného plynu má tvar kužele a nazývá se rázová vlna (Obrázek 4). Sklon rázové vlny β_SW je vždy větší než úhel tzv. Machův úhel μ, který by vznikal při pohybu nekonečně tenkého tělesa.

4: Vztah mezi úhlem rázové vlny a Machovým úhlem

Kritická rychlost

Jestliže ke snižování rychlosti nadzvukového proudu dochází pouze ve zužujícím se kanále, pak rychlosti zvuku lze dosáhnout pouze v nejužším místě kanálu. Pokud se tak stane, tak říkáme, že proudění dosáhlo v kanále kritické rychlosti V*.

Nadzvuková tryska

Nadzvukový difuzor

Chování nadzvukového proudění je tedy přesně opačné než proudění podzvukového, díky tomu dva tvarově totožné kanály na Obrázku 6 fungují zcela odlišně při podzvukovém a nadzvukovém proudění na vstupu. Zobrazený kanál se chová jako nadzvuková tryska, jestliže do kanálu vstupuje podzvukové proudění (Obrázek 6a), které zvyšuje svou rychlost až na M=1 v nejužším průřezu, za tímto průřezem se rychlost dále zvyšuje až na vysoce nadzvukovou výstupní rychlost. Naopak zobrazený kanál se chová jako nadzvukový difuzor, jestliže do kanálu vstupuje nadzvukové proudění, které snižuje svou rychlost na M=1 v nejužším průřezu, za kterým se rychlost dále snižuje až na nízkou podzvukovou rychlost, tím se transformuje kinetická energie nadzvukového proudu na tlakovou energii.

6: Příklady vlivu vstupní rychlosti na funkci kanálu proměnlivého průřezu

(a) Nadzvuková tryska, běžně nazývána jako Lavalova tryska^4.; (b) nadzvukový difuzor.

Rázové vlny

Stroje, ve kterých může docházet k nadzvukovým rychlostem lze reálně konstruovat jen pro konkrétní podmínky (lze dokázat, že poměr výstupního průtočného průřezu ku minimálnímu průřezu musí být pro rozdílná Machova čísla také rozdílná), při změně podmínek by bylo nutné měnit geometrii stroje, aby splňoval požadavky na přechod proudění z nadzvukového do podzvukového. To často není možné splnit a přechod se uskuteční v rozšiřující se části proudové trubice skokem, tj. skokovou změnou stavových veličin tedy rázovou vlnou, jen tak lze splnit podmínky Hugoniotovy věty (plynulý přechod není v takovém kanále možný). Přičemž existuje několik základních druhů rázových vln podle podmínek, za jakých vznikly, viz následující kapitoly.

Rankine-Hugoniotovy rovnice

Ztráta v rázové vlně nezávisí přímo na geometrii obtékaného tělesa, ale pouze na vlastnostech plynu a jeho rychlosti, což je patrné z Rankine-Hugoniotových rovnic pro stav plynu před a za vlnou, viz Rovnice 9 a také z výpočtu Úlohy 1.

9: Rovnice stavu plynu před a za kolmou rázovou vlnou

Rovnice jsou odvozeny pro stabilní kolmou rázovou vlnu a ideální plyn. Odvození rovnic je provedeno v Příloze 5.

Šikmá rázová vlna

Odklon proudu

Normálová rychlost

Tečná rychlost

Při průchodu proudění šikmou rázovou vlnou se jeho rychlost sníží (může být podzvuková i nadzvuková) a navíc dojde ke změně směru proudu o úhel δ, viz Obrázek 10. Přičemž pro normálové složky rychlosti šikmé rázové vlny V_1n, V_2n platí stejné vlastnosti jako pro proudění procházející kolmou rázovou vlnou, viz Úloha 2. Lze také dokázat rovnost tečných složek rychlosti V_1t=V_2t [Kadrnožka, 2004, s. 126-127].

10: Průchod stlačitelného prostředí šikmou rázovou vlnou

δ [°] Odklon proudu za rázovou vlnou od původního směru. Index _n označuje normálové složky rychlosti, Index _t označuje tečné složky rychlosti.

Úhel rázové vlny

Ztráty

Zvuková vlna

Jestliže je úhel β_SW stejný jako Machův úhel μ, pak musí platit V_1n=a₁ a jedná se pouze o zvukovou vlnu, což plyne z definice Machova úhlu. Dále lze dokázat, že k největší energetické ztrátě (nárůstu entropie) dochází při β_SW=90° – to znamená, že ztráty v šikmé rázové vlně jsou menší než v kolmé pro stejný tlakový poměr tlaků před a za vlnou.

Kumulace rázových vln

Při reálném nadzvukovém proudění místo kompresních vln vzniká kumulace šikmých rázových vln (Obrázek 12). Úhel šikmých rázových vln vznikajících za sebou se postupně zvětšuje tak, jak klesá Machovo číslo, takže se v určité vzdálenosti postupně slučují do jedné. Výsledná šikmá rázová vlna má odpovídá suočtu hybností sloučených rázových vln a má i menší úhel β_SW než první vlna.

12: Kumulace šikmých rázových vln

(a) stupňující se plocha; (b) vznik kompresních vln u pozvolna se zvedající plochy [Nožička, 2000]. CW-soustava kompresních vln.

Zředění rázové vlny

V letectví se provádí experimenty se snižování zvukových jevů způsobené rázovými vlnami při nadzvukových letech založené na rozdělení rázové vlny na několik dílčích vln (zředění rázové vlny, viz Obrázek 13). Tímto způsobem se zvýší úhel výsledné rázové vlny (poté co se setkají všechny rázové vlny od trupu letounu). Čím je totiž úhel rázové vlny větší (nejlépe 90°), tím je zvukový efekt od vlny menší [Hošek, 1962, s. 60] – což by umožňovalo dopravním letounům alespoň omezeně let vysokou rychlostí i nad obydlenými oblastmi.

13: Projekt Quiet Spike

Projekt se úspěšně zabýval možností snížit intenzitu zvukových jevů pomocí odstupňovaně prodloužené přídě letounu. Zde testování teleskopické přídě letounu F-15B [Creech, 2009].

Expanzní vlny

Pokud se nadzvukové proudění dostane do prostoru se zvyšujícím se průtočným průřezem musí expandovat do vyšší rychlosti, jak predikuje Hugoniotova věta. Taková nadzvuková expanze probíhá formou expanzních vln.

Odklon proudu

Zvyšující se průtočný průřez vytvářejí i tupé úhly na tělesech, například odtoková hrana projektilů, místa počátku zužovaní trupu letounů apod., viz Obrázek 16, na kterém je typická charakteristika obtékání tupého úhlu nadzvukovou rychlostí. Při obtékání tupých úhlů nadzvukovou rychlostí musí docházet k expanzi plynu z tlaku p₁ na tlak p₂ a ke zvýšení rychlosti proudu z V₁ na V₂, zároveň dojde i k vychýlení směru proudícího plynu o úhel δ od původního směru. V expanzní vlně probíhá pozvolná změna stavových veličin s malými ztrátami.

16: Obtékání tupého úhlu nadzvukovou rychlostí

ML-Machova čára (Mach line); Δ [m] délkový rozdíl.

Machova čára

Prandtl-Meyerovy funkce

Vznik expanzní vlny na Obrázku 16 iniciuje tlaková porucha na hraně S. Tato porucha se šíří rychlostí zvuku (takže se nemůže šířit proti proudu), která se šíří se pod Machovým úhlem μ₁. První proudnice zareaguje okamžitě a začne expandovat do tlaku nižšího změnou směru proudění ve směru poklesu tlaku. Vzdálenější proudnice expanduje až za hranou S, protože než k ní dorazí tlaková porucha urazí vzdálenost Δ. Hranice ML₁, na které se začne měnit směr proudění a plyn expandovat je tzv. Machova čára jejíž sklon je roven Machovu úhlu μ₁. Na první Machově čáře započne tedy expanze plynu. Při expanzi dochází ke změně Machova čísla a tedy i Machova úhlu. Expanze se ukončí na Machově čáře ML₂, na které proudící plyn dosáhne tlaku p₂. První a poslední Machova čára vytváří Machův klín, ve kterém expanze plynu probíhá. Přičemž hodnotu úhlu δ lze stanovit z Prandtl-Meyerovy funkce ν [ANON., 2010], viz Rovnice 17.

Zvukové a nadzvukové proudění

Kolmá rázová vlna

Šikmá rázová vlna

λ-rázová vlna se posouvá s roustoucí rychlostí směrem k odtokové hraně profilu, takže při dosažení rychlosti zvuku se dostane až k odtokové hraně a na nátokové hraně se začně formovat kolmá rázová vlna (Obrázek 19(a)). Při nadzvukové rychlosti se přetvoří čelní kolmá rázová vlna na šikmou a to samé se stane na odtokové hraně, kde se vytvoří dvě šikmé rázové vlny srážkou dvou nadzvukových proudů od sací a přetlakové strany profilu, viz Obrázek 19(b).

19: Obtékání čočkovitého profilu zvukovým a nadzvukovým prouděním

(a) rychlost zvuku před profilem; (b) nadzvuková rychlost před profilem [Kneubuehl, 2004, s. 78].

Raketoplán

Příkladem přechodu z transsonické do nadzvukové rychlosti je start raketoplánu Discovery (STS-114, 2005) na Obrázku 20. Vlevo je snímek v čase 50,87 s po startu (1,2 Mach, aerodynamický odpor dosahuje maxima), vpravo je snímek v čase 59,72 s (1,5 Mach aerodynamický odpor klesá.

20: Charakteristika obtékání raketoplánu stlačitelným prouděním během jeho startu

Zdroj fotografií [O’Farrell and Rieckhoff, 2011].

Glauert-Prandtlovo pravidlo

Součinitel vztlaku

Tlakový součinitel

Součinitel odporu

Kritické Reynoldsovo číslo

Laminární profil

Pro přepočet aerodynamických veličin získaných z měření při nestlačitelném proudění na situaci stlačitelného proudění lze použít Glauert-Prandtlova pravidlo, viz Rovnice 21. Tyto rovnice lze použít pouze pro rychlosti proudění nepřekračující kritické Machovo číslo ani kritické Reynoldsovo číslo – profily, u kterých proudění nepřekračuje kritické Reynoldsovo číslo se nazývají laminárními profily [Abbott and Doenhoff, 1959, s. 256 a s. 283-287], [Hošek, 1949, s. 52].

Z výše uvedeného je evidentní, že pro pro vyšší rychlosti obtékání postačují tenké profily, čehož si každý všimne u stíhacích nadzvukových letounů, které jsou štíhlejší než podzvukové stroje.

Profily pro vysoké rychlosti

U dobře navrženého profilu by měl být předvídatelný vznik jevů spojených s vysokou rychlostí a jejich vliv na aerodynamiku letu. Dobře předvídatelný je v tomto směru kosočtvercový profil. Expanzní vlny vznikají pouze na vrcholcích sací a přetlakové strany a λ-rázové vlny vznikají až u odtokové hrany profilu. Samozřejmě tento profil není vhodný pro nízké podzvukové rychlosti, takže se hledají různé kompromisy tvarů profilů podle toho, pro jaké rychlosti jsou primárně určeny, viz Obrázek 24.

24: Typy profilů vhodné pro vysoké rychlosti ve stlačitelném proudu

(a) transsonický profil; (b) supersonický (čočkový tvar); (c) supersonický (kosočtvercový tvar); (d) supersonický (lichoběžníkový tvar); (e) hypersonický.

Působiště vztlaku

Působiště odporu

Vysoké rychlosti způsobují také posun působiště vztlaku, které se posuvá se změnou Machova čísla [Hošek, 1949, s. 46, 240], současně se mění i velikost vztlaku, viz Obrázek 22. Z toho důvodu jsou moderní letouny vybaveny zařízeními pro změnu geometrie křídla či přesunu těžiště, a zejména při rychlostech kolem rychlosti zvuku mění náklon kvůli udržení takových nátokových úhlů, aby vztlak udržely v požadované velikosti – při velmi vysokých podzvukových rychlostech může být dokonce i záporný [Stever and Haggerty, 1966, Flight, s. 69].

Analytický výpočet

Analytické řešení v uzavřeném tvaru lze nalézt pro stlačitelného proudění v profilové mříži pouze pro případ jednorozměrného stlačitelného proudění v kanále – to je ekvivalentní analytickému návrhu trysek nebo difuzorů. Přesnějších výsledků, které berou v úvahu prostorových charakter proudění, lze dosáhnout numerickým modelováním pomocí výkonného výpočetního hardwaru a příslušného softwaru, viz Obrázek 26.

Úlohy

p [MPa]; t [°C].