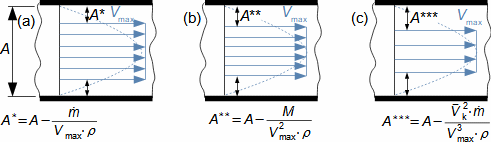
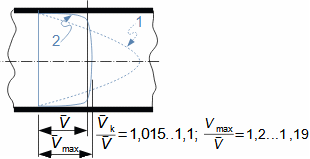
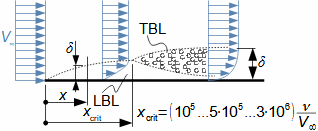
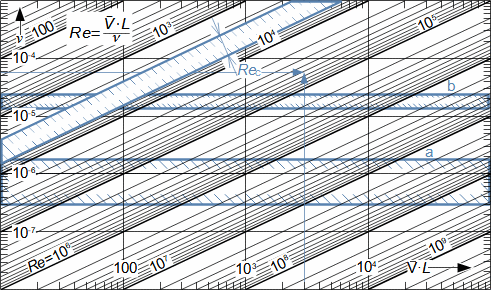
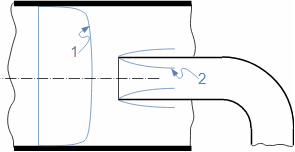
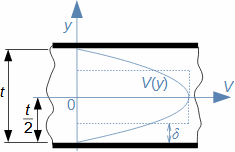
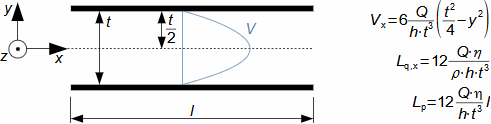
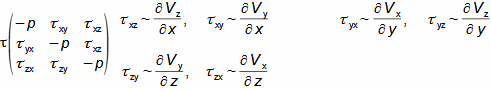fluid-dynamics.education
7.

VNITŘNÍ TŘENÍ TEKUTINY A VÝVOJ MEZNÍ VRSTVY

7.3 . . . . . . . . . . . . . .
Charakteristické rysy proudu tekutiny
7.4 . . . . . . . . . . . . . .
Čtyři definice střední rychlosti proudění
Rychlostní profil – Hmotnostní tok – Hybnost tekutiny – Kinetická energie
7.6 . . . . . . . . . . . . . .
Tři definice tloušťky mezní vrstvy
Pošinovací tloušťka – Impulsní tloušťka – Energetická tloušťka
7.7 . . . . . . . . . . . . . .
Definice viskozity a její hodnoty
Viskozita – Hodnoty viskozit
7.9 . . . . . . . . . . . . . .
Rovnice laminárního proudění
Navier-Stokesova rovnice – Eulerova rovnice hydrodynamiky – Poiseuilleův zákon – Střední rychlost
7.12 . . . . . . . . . . . . . .
Vývoj laminární mezní vrstvy a Reynoldsovo číslo
7.13 . . . . . . . . . . . . . .
Kolaps laminárního proudění a vývoj turbulentního proudění
Rychlostní profil – Kritické Reynoldsovo číslo
7.15 . . . . . . . . . . . . . .
Zánik turbulencí
7.16 . . . . . . . . . . . . . .
Úloha 1: Výpočet charakteristických tlouštěk mezní vrstvy
Úloha 2: Návrh tenzoru napětí v tekutině
Úloha 3: Výpočet viskozity směsi plynu
Úloha 4: Odvození rovnic pro laminární proudění mezi dvěma deskami
1.17 . . . . . . . . . . . . . .
Odkazy
7.18 - 7.35 . . . . . . . . .
Přílohy
Zobrazení v PDF
fluid-dynamics.education 
7.2
autor:
ŠKORPÍK, Jiří – LinkedIn.com/in/jiri-skorpik
datum vydání:       
Srpen 2023
název:
Vnitřní tření tekutiny a vývoj mezní vrstvy
sborník:
fluid-dynamics.education
provenience:
Brno (Česká republika)
email:
skorpik.jiri@email.cz

Copyright©Jiří Škorpík, 2023
Všechna práva vyhrazena.

Klíčová slovaKapitola: Charakteristické rysy proudu tekutiny
7.3

Charakteristické rysy proudu tekutiny

Vnitřní tření

Ztrátové teplo

Rychlostní profil

Mezní vrstva

Tlaková ztráta

Entropie proudící tekutiny se zvyšuje, což je způsobeno vnitřním třením tekutiny, které způsobuje, že část její kinetické energie se transformuje na vnitřní tepelnou energii tekutiny (dále označována jako ztrátové teplo). Dalšími projevy vnitřního tření je tlaková ztráta při proudění tekutiny kanálem a nižší rychlost proudění u okrajů kanálu a vyšší v jádru proudu – rozložení rychlosti tekutiny ve vyšetřovaném řezu kanálu nazýváme rychlostní profil. Nicméně rychlostní profil se vyvijí postupně. Na Obrázku 1 je znázorněn postupný vývoj rychlostního profilu tekutiny v potrubí na výtoku z nádoby při působení vnitřního tření. Vliv vnitřního tření započne až na vstupu do potrubí, kde dochází ke tření tekutiny o stěny kanálu, tato ztráta kinetické energie tekutiny se šíří směrem od stěn, a tím se postupně vyvíjí rychlostní profil. Současně se rychlost proudění v jádru proudu zvyšuje, aby byla zachována kontinuita proudu, protože v blízkosti stěn je rychlost naopak velmi nízká. Oblast ovlivněnou přítomnosti omočené stěny nazýváme mezní vrstvou proudění. V případě uzavřených kanálů se mezní vrstvy protilehlých stran, tak jak neustále rostou, po určité délce xe spojí.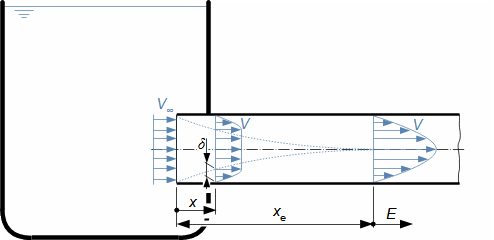

Vznik a vývoj rychlostního profilu v kanále
1: Vznik a vývoj rychlostního profilu v kanále
E-oblast plně vyvinuté mezní vrstvy. V [m·s-1] rychlost proudění ve vyšetřovaném místě kanálu; V∞ [m·s-1] rychlost proudění na vstupu do vyšetřovaného úseku kanálu; x vzdálenost od vstupu do potrubí; xe [m] vstupní délka; δ [m] tloušťka mezní vrstvy.

Ideální tekutina

Za účelem základních výpočtů složitých úloh v proudění a porovnávání definujeme ideální tekutinu, ve která neexistuje vnitřní tření a její tepelná kapacita je konstantní. Modely proudění s ideální tekutinou jsou k reálnému proudění tím bližší, čím je schopnost skutečné tekutiny produkovat vnitřní tření menší.

Klíčová slovaKapitola: Charakteristické rysy proudu tekutiny
7.4

Kapalné helium

Supratekutost

Nejblíže je ideální tekutině kapalné Helium, které při teplotách pod 2 K neprodukuje vnitřní tření, tato vlastnost se nazývá supratekutost. Supratekutost také umožňuje existenci navzájem protiproudých proudění v jednom kanále bez vzniku tření.

Laminární proudění

Turbulentní proudění

Wilkens et al., 2009

Vývoj mezní vrstvy a rychlostního profilu je ovlivněn druhem proudění. Existují dva druhy proudění podle principu vzjemné interakce mezi částicemi proudění a přenosu kinetické energie proudu mezi nimi. Jedná se o proudění laminární a proudění turbulentní. Při laminárním proudění vytváří tekutina rovnoběžná proudová vlákna, přičemž tato vlákna po sobě klouzají (v rámci vlákna vytváří tekutina drobné víry). Tekutina v sousedních proudových vláknech se nepromíchává. Při tubuletním proudění již nelze identifikovat jednotlivá proudová vlákna a pohyb elementráních částic tekutiny je náhodný. Na Obrázku 2 jsou uvedeny trajektorie částic, které jsou unášeny laminárním proudem a turbulentním proudem, viz také fotografie v [Wilkens et al., 2009]. Tyto částice jsou současně výrazně hmotnější než molekuly tekutiny, aby nemohla být ovlivněna Brownovým pohybem, ale současně na ně nemá významný vliv gravitační zrychlení. Nicméně i při turbulentním proudění převládají nišší rychlosti v blízkosti stěn a vyšší v jádru proudu. O tom za jakých okolností lze očekávat laminární nebo turbuletní proudění pojednává kapitola Kolaps laminárního proudění a vývoj turbulentního proudění.

2: Rozdíl mezi laminárním a turbulentním prouděním
(a) typická charakteristika laminárního proudu a jeho rychlostní profil; (b) typická charakteristika turbuletniho proudu a jeho rychlostní profil.

Teorie vnitřního tření, respektive mezní vrstvy, objasňuje vznik tlakové ztráty, chování tekutiny při proudění potrubím nebo zvýšení odporu při obtékání těles.

Čtyři definice střední rychlosti proudění

Velké množství parametrů proudu tekutiny se počítá ze střední rychlost proudění, která může být vztažena k rychlostnímu profilu, k hmotnostnímu toku, k hybnosti tekutiny a nebo ke kinetické energii tekutiny.

Klíčová slovaKapitola: Čtyři definice střední rychlosti proudění
7.5

Rychlostní profil

Střední rychlost proudění odvozená z rychlostního profilu odpovídá střední hodnotě rychlostního profilu, viz Vzorec 3c.

3: Příklady rychlostních profilů a středních rychlostí proudění
(a) rychlostní profil mezi dvěma deskami v případě proudění bez tření; (b) rychlostní profil mezi dvěma deskami reálné tekutiny. A [m2] průtočný průřez; ek [J·kg-1] průměrná hodnota kinetická energie tekutiny; M [N] hybnost tekutiny v kanále; m• [kg·s-1] hmotnostní tok; V [m·s-1] místní rychlost tekutiny; V‾ [m·s-1] střední rychlost proudění; y [m] souřadnice kolmá na směr proudění.

Hmotnostní tok

Střední rychlost proudění odvozená z hmotnostního toku ve vyšetřovaném kanále je definována Vzorcem 3d. Je to tedy taková rychlost proudění, při které za jednotku času proteče kanálem stejné množství tekutiny odpovídající hmotnostnímu toku – jedná se nejčastěji užívanou střední rychlost proudění.

Hybnost tekutiny

Střední rychlost proudění odvozená z hybnosti tekutiny ve vyšetřovaném kanále je definována Vzorcem 3e. Je to tedy taková rychlost tekutiny, při které by dosahovala stejné hybnosti (síla, kterou působí paprsek tekutiny na kolmou desku) jako skutečný proud tekutiny s rychlostním profilem.

Kinetická energie

Střední rychlost proudění odvozená z kinetické energie tekutiny ve vyšetřovaném kanále je definována Vzorcem 3f. Při této rychlosti by proud dosahoval stejného výkonu jako skutečný proud s rychlostním profilem.

Pro případ nestlačitelné tekutiny se hodnoty střední rychlosti stanovené z rychlostního profilu a hmotnostního toku rovnají (V‾m=V‾profil). Druhá nejpoužívanější definice střední rychlosti proudění v technické praxi je ta, která vychází z kinetické energie tekutiny – používá se v energetických bilancí, například pomocí Bernoulliho rovnice, ve které vystupuje kinetická energie tekutiny.

Klíčová slovaKapitola: Tři definice tloušťky mezní vrstvy
7.6

Tři definice tloušťky mezní vrstvy

Tloušťka mezní vrstvy se vyhodnocuje z pohledu jejího vlivu na hmotnostní tok, hybnost a energii vyšetřovaného proudu. Odtud rozlišujeme tři charakteristické tloušťky mezní, které jsou také použity při řešení Úlohy 1.

Pošinovací tloušťka

Hmotnostní tok

Ekvivaletní průtočný průřez, kterým by protékala pracovní tekutina maximální rychlostí a hmotnostním toku rovnající se rozdílu mezi průtokem bez tření a skutečném průtoku se nazýva pošinovací tloušťka mezní vrstvy, viz Rovnice 4a.

Charakteristické tloušťky mezní vrstvy pro případ proudění mezi dvěma deskami
4: Charakteristické tloušťky mezní vrstvy pro případ proudění mezi dvěma deskami
(a) pošinovací tloušťka; (b) impulsní tloušťka; (c) energetická tloušťka; (d) definice hranice ovlivněné oblasti v případě obtékání profilů. A* [m2] průtočný průřez pošinovací tloušťky mezní vrstvy; A** [m2] průtočný průřez impulsní tloušťky mezní vrstvy; A*** [m2] průtočný průřez energetické tloušťku mezní vrstvy; Vmax [m·s-1] maximální rychlost proudění; V∞ [m·s-1] nátoková rychlost (rychlost před obtékaným profilem). Rovnice jsou odvozeny v Příloze 5.

Impulsní tloušťka

Hybnost

Ekvivaletní průtočný průřez, kterým by protékala pracovní tekutina maximální rychlostí o hybnosti rovnající se rozdílu mezi hybností tekutiny bez tření a skutečnou hybností tekutiny se nazýva impulsní tloušťka mezní vrstvy, viz Rovnice 4b.

Energetická tloušťka

Kinetická energie

Ekvivaletní průtočný průřez, kterým by protékala pracovní tekutina maximální rychlostí o stejné kinetické energie jako je rozdíl mezi kinetickou energií tekutiny při proudění bez tření a kinetickou energii tekutiny při proudění se třením se nazývá energetická tloušťka mezní vrstvy, viz Vzorec 4c.

Profil

Nátoková rychlost

Charakteristické tloušťky mezní vrstvy v okolí osamocených profilů stanovují k nátokové rychlosti, přičemž hranice ovlivněné oblasti, ke které se stanovuje průtok, je ve vzdálenosti, ve které je rychlost proudění už velmi blízká rychlosti před ovlivněnou oblastí (dosahuje 99 % maximální rychlosti), viz Obrázek 4d.

Klíčová slovaKapitola: Tři definice tloušťky mezní vrstvy
7.7

Uvedené definice charakteristických tlouštěk se používají při porovnávání různých typů kanálu mezi sebou z pohledu rychlostí, hybnosti a energetických ztrát, protože jsou aplikace, kde je důležitá, například, co nejmenší ztráta hybnosti a u jiné energetická ztráta a podobně.

Definice viskozity a její hodnoty

Vliv vnitřního tření na rychlostní profil při laminárním proudění lze kvalifikovat pomocí veličiny zvané dynamická viskozita (zkráceně jen viskozita). Hodnot viskozit vyšetřovaných tekutin se používají pro výpočet parametrů proudu včetně tlakové ztráty.

Viskozita

Dynamická viskozita

Kinematická viskozita

Issac Newton

Dynamická viskozita je poměr mezi tečným napětím a tenzorem rychlosti, viz definiční Rovnice 5. Tuto definici zavedl Issac Newton na základě jednoduchého experimentu s vnitřním třením tekutiny, který je popsán v Příloze 6.

5: Definice viskozity
F [N] třecí síla působící na element; η [Pa·s] dynamická viskozita pracovní tekutiny; τ [Pa] tečné (smykové) napětí mezi proudovými vlákny způsobené třecí silou (tření mezi proudnicemi); ν [m2·s-1] kinematická viskozita; S [m2] třecí plochy mezi vyšetřovanými vlákny.

Newtonovská tekutina

Nenewtonovská tekutina

Viskózní tekutina

Tekutiny, u kterých lze uplatnit výše uvedenou definici viskozity nazýváme newtonovské tekutiny a naopak tekutiny, ve kterých se viskozita mění s rychlostí nazýváme nenewtonovské tekutiny (tekutiny obsahující větší shluky molekul jako koloidní roztoky, suspenze, emulze gely apod.).

Newtonův zákon viskozity

Bird, 1965

Definice viskozity zapsaná Vzorcem 5 vychází z velmi jednoduchého případu proudění v rovině. Jestliže vyšetřujeme proudění prostorové, kdy se mění rychlostní profil ve více směrech, musíme vycházet z tenzoru tečných napětí v tekutině od vnitřního tření tekutiny (viz Úloha 2). Vztahy mezi jednotlivými tečnými napětími a viskozitou při proudění v prostoru se nazývají Newtonův zákon viskozity, který je uveden například v [Bird et al., 1965] pro různé soustavy souřadnic.

Klíčová slovaKapitola: Definice viskozity a její hodnoty
7.8

Hodnoty viskozit

Viskozimetr

Viskozita vody

Viskozita vzduchu

Redukovaná viskozita

Kritická viskozita

Bird, 1965

Dynamická viskozita tekutin se měří pomocí viskozimetrů, kterých je několik typů. Výsledky měření se uvádí do termodynamických tabulek, které se využívají při výpočtech. Problém získání komplexních dat hodnot viskozity je v tom, že viskozita tekutin závisí na teplotě a tlaku. S rostoucí teplotou dynamická viskozita kapalin klesá a s rostoucím tlakem vzrůstá. Vliv tlaku je u většiny kapalin nevýznamný, vyjma velmi vysokých tlaků v řádech megapascalů. Dynamická viskozita plynů s rostoucí teplotou vzrůstá a je nezávislá na tlaku, vyjma extrémně nízkých nebo naopak vysokých tlaků. Z těchto důvodů se uvádí dynamické viskozity tekutiny pro technické účely pouze v závislosti na teplotě, viz Tabulky 6, 7 vody a páry a Tabulky 9, 10 suchého a vlhkého vzduchu. V případě nedostaku dat lze vypočítat přibližně viskozitu jako součin redukované a kritické viskozity. Redukovaná viskozita je funkcí tlaku a teploty, viz grafy v [Bird et al., 1965]. Kritická viskozita je viskozita látky v kritickém bodě.

t       0 10 20 30 40 50 60 70 80
η       1770,2 1303,9 1001,9 797,3 652,6 546,8 466,5 404,2 354,7
ν       1769,7 1303,7 1003,3 800,46 657,46 553,2 474,28 413,22 364,84
t       90 100 110 120 130 140 150 160 170
η       314,7 281,8 254,7 232,05 212,9 196,54 182,46 170,24 159,55
ν       325,87 293,92 267,84 246,05 227,74 212,22 198,97 187,6 177,78
6: Viskozita vody při tlaku 101 325 Pa
t [°C] teplota; η [μPa·s]; ν [nm2·s-1]. Hodnoty od teploty 100 °C a výše jsou pro sytou vodu, tedy při vyšším tlaku odpovídající syté kapalině.
t       0 10 20 30 40 50 60 70 80
η       9,24 9,461 9,7272 10,01 10,307 10,616 10,935 11,26 11,592
ν       1778 1005,8 561,81 329,12 201,15 127,68 83,837 56,747 39,474
t       90 100 110 120 130 140 150 160 170
η       11,929 12,269 12,612 12,956 13,301 13,647 13,992 14,337 14,681
ν       28,141 20,511 15,251 11,547 8,8853 7,9770 5,4912 4,3983 3,5615
7: Viskozita syté vodní páry
t [°C]; η [μPa·s]; ν [nm2·s-1].

Viskozita směsi

V technické praxi se velmi často pracuje se směsmi, jak plynnými, tak kapalnými, které se skládají ze dvou nebo více čistých látek. Viskozita směsi závisí na molárních koncentracích jednotlivých složek směsi, viz Rovnice 8 a také Úloha 3.

Rovnice pro výpočet viskozity směsi
8: Rovnice pro výpočet viskozity směsi
ηi [Pa·s] dynamická viskozita jednotlivé složky směsi; δi [1] molární zlomek jednotlivé složky směsi. Rovnice je platná pro případy, kdy jsou jednotlivé viskozity nezávislé na parciálních tlacích jednotlivých složek.
Klíčová slovaKapitola: Definice viskozity a její hodnoty
7.9
t       -20 0 10 20 40 60 80 100 150
η       16,28 17,08 17,75 18,24 19,04 20,10 20,99 21,77 23,83
ν       11,93 13,70 14,70 15,70 17,60 19,60 21,70 23,78 29,50
t       200 300 400 500 600 700 800 900 1000
η       25,89 29,70 33 36,20 39,10 41,70 44,40 46,60 49,30
ν       35,82 48,20 63 79,30 96,80 115 135 155 178
9: Viskozita suchého vzduchu při 0,1 MPa
t [°C]; η [μPa·s]; ν [μm2·s-1].
t 10 20 40 60 80 100
ϕ η η η η η η
0,2 17,73 18,20 18,91 19,75 20,15 20,12
0,4 17,71 18,16 18,79 19,43 19,45 18,96
0,6 17,69 18,12 18,67 19,13 18,86 18,10
0,8 17,67 18,09 18,56 18,85 18,35 17,43
1 17,65 18,05 18,45 18,59 17,91 16,90
ν ν ν ν ν ν
0,2 14,67 15,63 17,35 18,86 19,77 19,66
0,4 14,63 15,56 17,11 18,17 18,16 16,75
0,6 14,60 15,49 16,87 17,53 16,80 14,60
0,8 14,57 15,43 16,64 16,93 15,62 12,93
1 14,54 15,36 16,42 16,38 14,60 11,61
10: Viskozita vlhkého vzduchu při 0,1 MPa
t [°C]; η [μPa·s]; ν [μm2·s-1]; ϕ [1] relativní vlhkost vzduchu

Rovnice laminárního proudění

Základní parametry laminárního proudění lze určit pomocí Navier-Stokesovy rovnice. Přičemž speciálnímy tvary Navier-Stokesovy rovnice pro případ nevýznamného vlivu viskozity je i Eulerova rovnice hydrodynamiky. Navíc lze pomocí Navier-Stokesovy rovnice odvodit rovnice pro tlakovou ztrátu nebo ztrátové teplo pro případy kanálů jednoduchých tvarů, například Poiseuilleův zákon pro tlakovou ztrátu v kruhovém potrubí, vztah mezi střední rychlostmi určené z hmotnostního toku a kinetické energie tekutiny apod.

Navier-Stokesova rovnice

Claude-Louis Navier

George Gabriel Stokes

Bird, 1965

Množství ztrátového tepla roste ve směru proudění, odtud a pomocí definice viskozity, lze odvodit rovnici laminárního pohybu tekutiny nazývanou také jako Navier-Stokesovu rovnicí, viz Rovnice 11. Uvedenou rovnici na základě kinetiky pohybu molekul odvodil francouzský inženýr Claude-Louis Navier (1785-1836). Irský matematik George Gabriel Stokes (1819-1903) je v názvu přidán na počest, protože s rovnicí dále experimentoval a hlouběji popsal její možnosti, i když vědců, kteří ji rozvinuli bylo více.

Klíčová slovaKapitola: Rovnice laminárního proudění
7.10
11: Navier-Stokesova rovnice
g [m·s-2] gravitační zrychlení; grad Lq [J·kg-1·m-1] gradient ztrátového tepla (množství ztrátového tepla uvolněného v 1 kg tekutiny při posuvu o 1 m daným směrem); p [Pa] tlak; s→ [m] jednotkový směrový vektor; (V·∇)V [J·kg-1·m-1] změna (gradient) kinetické energie ve směru proudění. Rovnice je odvozena pro případ ustáleného laminárního proudění viskózní tekutiny při konstantní hustotě v Příloze 7, pro obecný případ nestacionárního proudění s proměnnou hustotou je Navier-Stokesova rovnice odvozena v [Bird et al., 1965], kde je označována jako rovnice pohybu.

Ztrátové teplo

Teplo znovu využité

Ztrátové teplo Lq je příčinou rostoucí entropie tekutiny. Zvýšení ztrátového tepla může docházet nejen při tření, ale i při víření mezi jednotlivými proudnicemi. U plynů se část ztrátového tepla, respektive vnitřní tepelné energie může zpět transformovat na tlakovou, kinetickou nebo potenciální energii a práci. To je způsobeno tím, že při zvýšení teploty se zvětší měrný objem plynu. Pro tuto energii se používá v teorii lopatkových strojů pojmu teplo znovu využité [Škorpík, 2024]. Z rovnice ztrátového tepla také plyne, že plyn při velmi malé hustotě, respektive tlaku, může mít tekutina velmi vysoké vnitřní tření.

Potenciální proudění

Laminární proudění není potenciální proudění [Škorpík, 2023], protože rotor vektoru rychlosti je různý od nuly, respektive vektor rychlosti není gradientem potenciální veličiny. Nicméně rychlost laminárního proudění je potenciální veličina, protože ji lze určit pouze zadáním souřadnic.

Eulerova rovnice hydrodynamiky

Eulerova rovnice hydrodynamiky (Rovnice 12) je rovnice odvozená ze silové rovnováhy elementu tekutiny bez uvažování vlivu třecích sil na tento element. Lze ji jednoduše získat z Rovnice 11 pro případ, že levá strana se rovná 0. Z Rovnice 12 je dobře patrné, že skalární násobek vektoru rychlosti a divergence rychlosti (V·∇)V je zrychlení tekutiny, které lze rozepsat do tvaru Rovnice 12(vlevo) jako součet gradientu kinetické energie rychlosti a vektorových součinů rychlosti – to znamená, že laminární proudění není potenciální, protože v případě potenciálního proudění je zrychlení rovno pouze gradientu kinetické energie.

Eulerova rovnice hydrodynamiky
12: Eulerova rovnice hydrodynamiky
Odvození Eulerovy rovnice hydrodynamiky pro vírové proudění a souvislosti s potenciálním prouděním jsou uvedeny v Příloze 8.
Klíčová slovaKapitola: Rovnice laminárního proudění
7.11

Poiseuilleův zákon

Potrubí

Gotthilf Hagen

Jean Poiseuille

Johann Nikuradse

Odvození rovnic pro tlakovou ztrátu a rychlost tekutiny při laminárním proudění v kanálech jednoduchých tvarů není pomocí Navier-Stokesovy rovnice obtížné, viz Úloha 4 pro proudění mezi dvěma deskami a Rovnice 13 pro potrubí kruhového průřezu. Rovnice pro laminární proudění kruhovým průřezem poprvé odvodil německý inženýr Gotthilf Hagen (1797-1884) a francouzský fyzik Jean Poiseuille (1797-1869), proto se někdy označují jako Poiseuilleův zákon. Platnost této rovnice (mimo velmi krátkých úseků) potvrdil německý inženýr původem z Gruzie Johanna Nikuradseho (1894-1979).

13: Parametry laminárního proudění v potrubí
Lp [Pa] tlaková ztráta na vyšetřované délce potrubí; l [m] délka potrubí; re [m] vnitřní poloměr potrubí; Q [m3·s-1] objemový tok; r [m] vzdálenost vyšetřovaného poloměru od středu (osy) potrubí; V [m·s-1] axiální složka rychlosti (ve směru osy potrubí). Vztah je odvozený v Příloze 9 pro případ ustáleného proudění nestlačitelné tekutiny v kruhového potrubí, při vynechání vlivu potenciální energie z Navier-Stokesovy rovnice.

Střední rychlost

Kinetická energie

Odvození rovnic pro střední rychlost laminárního proudění podle jejich definičních Rovnic 3 je pro jednoduché tvary kanálů snadný, viz Rovnice 13 a Rovnice 14 pro střední rychlosti v potrubí a laminární proudění mezi dvěma deskami.

14: Vztah mezi střední rychlosti proudění a kinetickou energií
(a) rovnice střední rychlosti proudění při laminárním proudění tekutiny mezi dvěma deskami; (b) rovnice střední rychlosti proudění při laminárním proudění tekutiny trubkou. Rovnice byly odvozeny pro konstantní hustotu tekutiny ρ=konst. Odvození rovnic je uvedeno v Příloze 10.
Klíčová slovaKapitola: Vývoj laminární mezní vrstvy a Reynoldsovo číslo
7.12

Vývoj laminární mezní vrstvy a Reynoldsovo číslo

Rychlostní profil

Vstupní délka

Reynoldsovo číslo

Rychlostní profil po celé vyšetřované délce nemusí být stálý, zvláště jedná-li se o vstupní úsek do zkoumaného kanálu/potrubí, ve kterém teprve dochází ke vzniku mezní vrstvy, viz Obrázek 1. Vstupní délka kanálu xe, na které dochází k vývoji mezní vrstvy, je funkcí tvaru kanálu a poměru mezi dynamickým tlakem a smykovým napětím v tekutině, který označujeme jako Reynoldsovo číslo Re, viz Vzorce 15.

Výpočet vstupní délky kanálu a Reynoldsovo číslo
15: Výpočet vstupní délky kanálu a Reynoldsovo číslo
Ch [m] součinitel hydraulické vstupní délky; L [m] charakteristický rozměr; Re [1] Reynoldsovo číslo (do vzorce pro xe dosazujeme Re při plně vyvinuté mezní vrstvě) – vzorec pro Reynoldsovo číslo je odvozen v Příloze 11. Popisy jednotlivých veličin následují.

Součinitel hydraulické vstupní délky

Joseph Boussinesq

Ludwig Schiller

Bauer, 1950

Latif, 2006

Hodnoty součinitele hydraulické vstupní délky pro trubku kruhového průřezu jsou přibližně v rozsahu Ch≈0,025...0,065 – hodnotu 0,065 odvodil francouzský fyzik a matematik Joseph Boussinesq (1842-1929), hodnotu 0,025 německý fyzik Ludwig Schiller (1882-1961). Přičemž lze říci, že vyšší hodnoty odpovídají kratším a nižší delším vstupním úsekům (shrnuto v [Bauer et al., 1950, s. 143]). Součinitelé Ch pro kanály jiných než kruhových průřezů jsou uvedeny v [Latif, 2006, s. 208] a výběr v Tabulce 16.

t=h h=2·t h=4·t h·t-1≈∞
Ch 0,09 0,085 0,075 0,011
16: Součinitelé hydraulické vstupní délky kanálů obdelníkového tvaru
Ch [m]; h [m] delší strana obdélníku; t [m] kratší strana obdélníku.

Charakteristický rozměr (ekvivalentní průměr)

Omočený obvod

Profil

Tětiva

Charakteristický rozměr ve Vzorcích 15 zohledňuje rozměr průtočného kanálu, nebo obtékaného tělesa. Je to rozměr, ke kterému se provádí případná měření. Charakteristický rozměr uzavřených kanálů je nejčastěji definován Vzorecem 17 – v případě kruhového průřezu je to průměr, proto se charakteristický rozměr nazývá i ekvivalentním průměrem. Existuje ale i řada atypických případů, u kterých je použita jiná definice charakteristického rozměru. Obecně charakteristickým rozměrem těles bývá rozměr, který má největší vliv na proudění (například u lopatkových profilů je to délka tětivy).

Klíčová slovaKapitola: Vývoj laminární mezní vrstvy a Reynoldsovo číslo
7.13
17: Definiční vzorec charakteristického rozměru průtočného průřezu
A [m2] průtočná plocha; u [m] omočený obvod kanálu (obvod průtočného průřezu kanálu, který je ve styku s proudící tekutinou).

Kolaps laminárního proudění a vývoj turbulentního proudění

Kritická rychlost

Mezi proudnicemi laminárního proudění působí na elementy tekutiny dvojice sil (viz Obrázku 5), tato dvojice sil uvadí elementy do rotace. To znamená, že mezi jednotlivými proudnicemi vzniká řada drobných vírů, které svou energii maří třením, respektive jejich kinetická energie je konstantní, nicméně při vyšších rychlostech energie ve vírech postupně roste. Nakonec mohou víry získat takovou energii, že začnou narušovat hranice proudnic a dochází k vzájemnému promíchávání proudu a sdílení energií. Nastává turbulentní proudění. Rychlost, při které toto nastane se nazývá kritická rychlost laminárního proudění. Při této rychlosti setrvačné síly částic převažují nad třecí silou.

Rychlostní profil

Střední rychlost

Bird, 1965

Turbulentní rychlostní profil je charakteristický tím, že u něj nejsou patrné tak výrazné rozdíly mezi rychlosti v jádru a na okrajích proudu jako u laminárního rychlostního profilu, viz Obrázek 18. To je dáno migrací částic tekutiny a tedy i kinetické energie v celém průtočném průřezu (viz Obrázek 2). Tvar rychlostního profilu turbulentního proudění lze stanovit podle rovnic uvedených například v [Bird et al., 1965].

Turbulentní rychlostního profil v potrubí
18: Turbulentní rychlostního profil v potrubí
1-rychlostní profil laminárního proudění; 2-rychlostní profil turbulentního proudění. Vmax [m·s-1] maximální rychlost v turbulentním profilu. Data pro poměry rychlostí [Maštovský, 1964, s. 78], [Mikula et al., 1974, s. 57].

Turbulence

Mezní vrstva

Potrubí

Kritická rychlost proudění nezaručuje existenci turbulencí v celém vyšetřovaném objemu tekutiny. Turbulentní proudění se vyvijí z laminárního proudění při nárůstu setrvačných sil v mezní vrstvě, viz Obrázek 20. Například plně vyvinuté turbulentní proudění v potrubí se nachází až v oblasti potrubí vzdálené od ústí 10 až 60 průměrů potrubí [Jícha, 2001, s. 66].

Klíčová slovaKapitola: Kolaps laminárního proudění a vývoj turbulentního proudění
7.14

Turbulizátory

Odtržení proudu

Délka úseku, na které začne proudění turbulizovat také záleží na geometrii vstupu, kde se mohou narušovat proudnice o vstupní hrany a také na drsnosti povrchu, na tomto principu fungují tzv. turbulizátory, která mají za úkol vyvolat turbulentní proudění co nejdříve, například pro potřeby promíchávání proudů, nebo pro potřeby rovnoměrného rozložení kinetické energie proudu jako jedno z opatření ke snížení citlivosti na odtržení proudění od stěn difuzorů a pod.

Vývoj turbulencí při obtékání desky
20: Vývoj turbulencí při obtékání desky
LBL-laminární mezní vrstva (laminar boundary layer); TBL turbulentní mezní vrstva (turbulent boundary layer). δ [m] lokální tloušťka mezní vrstvy; x [m] vzdálenost od okraje; xcrit [m] začátek přechodu z laminární do turbulentní mezní vrstvy (vzorec z [Latif, 2006, s. 296]).

Kritické Reynoldsovo číslo

Hodnotu kritické rychlosti, při které začně docházet zhroucení laminárního do turbulentního proudění lze určit z Reynoldsova čísla při kterém tento děj nastane, protože vznikající víry budou narušovat proudová vlákna tím více, čím větší bude poměr dynamického tlaku proudící tekutiny (setrvačná síla) ku smykovému napětí (třecí síla) v tekutině. Tato hodnota Reynoldsova čísla se nazývá kritické Reynoldsovo číslo ReC.

Potrubí

Hodnota kritického Reynoldsova čísla pro potrubí získána experimenty je ReC=2320. Nicméně, ale v některých případech může být i vyšší, proto se rozmezí Re=2320 do Re=5000 až 6000 označuje jako přechodová oblast. To znamená, že při těchto hodnotách je jistá pravděpodobnost jak pro laminární tak turbuletní proudění. Od Re=6000 (tzv. horní kritické Reynoldsovo číslo) je proudění vždy turbulentní. Je třeba zdůraznit, že v praxi tyto hodnoty budou nižší, protože zde uvedené hodnoty pochází z měření v laboratořích na dokonale uložených potrubích bez vibrací.

Potrubí

Laminární proudění

Na Obrázku 19 je nomogram pro výpočet Reynoldsova čísla s vyznačením přechodové oblasti při proudění v potrubí. Z nomogramu mimo jiné vyplývá, že laminární proudění v běžných případech nastává jen za velmi vysokých hodnot kinematických viskozit a nízkých rychlostí – nejpravděpodobněji se sním lze setkat u vzduchovodů malých průměrů – jinak jsou Reynoldsova čísla výrazně větší než kritické Reynoldsovo číslo.

Klíčová slovaKapitola: Kolaps laminárního proudění a vývoj turbulentního proudění
7.15
Nomogram pro odečet Reynoldsových čísel
19: Nomogram pro odečet Reynoldsových čísel
V‾ [m·s-1]; L [mm]; ν [m2·s-1]; Re [1]. a-rozsah kinematických viskozit vody mezi 0 °C a 100 °C; b-rozsah kinematických viskozit suchého vzduchu mezi 0 °C a 100 °C. ReC [1] rozsah kritických Reynoldsových čísel pro potrubí.

Zánik turbulencí

Mezní vrstva

Laminární proudění

Laminátor

Turbulentní proudění může zpět přejít do lamirnárního, jestliže klesne Reynoldosvo číslo pod kritické Reynoldsovo číslo. Například, vložíme-li do turbulentního proudění desku, tak na jejích obou stranách se vytvoří laminární mezní vrstva, viz Obrázek 20. Další příkladem je změna průměrů potrubí, jak je naznačeno na Obrázku 21. V tomto případě je nasáván turbulentní proud vloženou trubkou v jejiž ústí se vytváří laminární mezní vrstva, která, jestliže je v tomto kanálu Reynoldsovo číslo dostatečně nízké, se může spojit a může vytvořit laminární profil v celém průřezu. Stejný efekt vzniku laminární vrstvy lze sledovat i při proudění v lopatkových kanálech, i když na vstupu je turbulentní proud. Vložky v proudu, ve kterých má vzniknout nebo udržet laminární vrstva se nazývá laminátor.

Klíčová slovaKapitola: Zánik turbulencí
7.16
Přechod turbulentního proudění do laminárního
21: Přechod turbulentního proudění do laminárního
1-plně vyvinutý turbulentní profil; 2-oblasti vzniku laminárních mezních vrstev.

Úlohy

Úloha 1:
Vypočítejte charakteristické tloušťky mezní vrstvy pro proudění mezi dvěma deskami, jestliže by byl rychlostní profil parabolický. Maximální rychlost proudění, šířku, výšku kanálu a hustotu tekutiny si zvolte. Řešení úlohy je uvedeno v Příloze 1.
Parabolický rychlostní profil mezi dvěma deskami
t [m] vzdálenost desek; δ [m] charakteristická tloušťka mezní vrstvy.
§1   zadání:   Vmax; t; h; ρ §4   výpočet:   M; A**; δ**
§2   výpočet:   A; m; V¯ §5   výpočet:   V¯k; A***; δ***
§3   výpočet:   A*; δ*    
Popisek symbolů je v Příloze 1.
Úloha 2:
Určete tvar tenzoru napětí v tekutině při laminárním proudění mezi dvěma deskami, jestliže ve vyšetřovaném bodě je tlak p. Řešení úlohy je uvedeno v Příloze 2.
tenzor napětí v tekutině
Úloha 3:
Určete viskozitu směsi dusíku N2 a kyslíku O2 při standardních podmínkách. Molární zlomek dusíku pro tuto směs je 0,785. Řešení úlohy je uvedeno v Příloze 3.
§1   zadání:   δN2 §3   výpočet:   δO2
§2   odečet:   ηi §4   výpočet:   η
Popisek symbolů je v Příloze 3.
Klíčová slovaKapitola: Úlohy
7.17
Úloha 4:
Stanovte rovnice pro ztrátové teplo, tlakovou ztrátu a rychlost pro případ ustáleného plně vyvinutého laminárního proudění nestlačitelné tekutiny mezi dvěma deskami. Řešení úlohy je uvedeno v Příloze 4.
Rovnice laminárního proudění mezi deskami

Odkazy

ŠKORPÍK, Jiří, 2023, Technická matematika, engineering-sciences.education, Brno, [online], ISSN 1804-8293. https://engineering-sciences.education/technicka-matematika.html
ŠKORPÍK, Jiří, 2024, Termodynamika tepelných turbín, Transformační technologie, Brno, [online], ISSN 1804-8293. https://turbomachinery.education/termodynamika-tepelnych-turbin.html
BAUER, František, Oldřich BRŮHA a Zbyněk JAŇOUR, PEŠEK, Rudolf, ed., 1950, Základy proudění, Vědecko-technické nakladatelství, Praha.
BIRD, Byron, STEWART, Warren, LIGHTFOOT, Edwin, 1960, Transport phenomena, John Wiley & Sons, New York. (České vydání: BIRD, Byron, STEWART, Warren, LIGHTFOOT, Edwin, 1968, Přenosové jevy: sdílení hybnosti, energie a hmoty, Academia, Praha)
JÍCHA, Miroslav, 2001, Přenos tepla a látky, Vysoké učení technické v Brně, Brno, ISBN 80-214-2029-4.
LATIF, Jiji, 2006, Heat Convention, Springer-Verlag, Berlin, ISBN-10 3-540-30692-7.
MAŠTOVSKÝ, Otakar, 1964, Hydromechanika, Statní nakladatelství technické literatury, Praha.
MIKULA, Julius, KOČKA, Jaroslav, ŠKRAMLÍK, Emanuel, ŠTAUBER, Zdeněk, VESELÝ Adolf, OBR, Jan, 1974, Potrubí a armatury, Státní nakladatelství technické literatury, Praha.
WILKENS, Andreas; DREISEITL, Herbert; GREENE, Jennifer; JACOBI, Michael; LIESS, Christian SCHWENK, Wolfram, 2009, Wasser bewegt: Phänomene und Experimente, Haupt Verlag, Bern, ISBN 978-3258075211. (České vydání: Andreas; DREISEITL, Herbert; GREENE, Jennifer; JACOBI, Michael; LIESS, Christian SCHWENK, Wolfram, 2009, Voda v pohybu - úžas v nás: pozorování a pokusy, Malvern, Praha, ISBN: 978-80-7530-069-0)
©Jiří Škorpík, LICENCE