Vznik tlakové ztráty při proudění tekutiny a její výpočet

Škorpík, Jiří

Klíčová slovaKapitola: Popis vzniku tlakové ztráty a základních pojmů

1.3

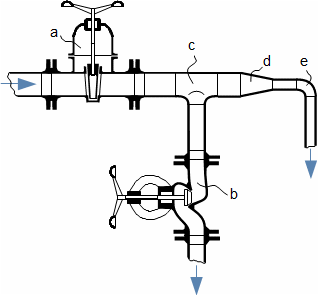
Popis vzniku tlakové ztráty a základních pojmů

Vnitřní tření

Při proudění tekutin vzniká tření o povrch průtočného kanálu a obtékaných těles i tření uvnitř tekutiny (tzv. vnitřní tření). Třením ztrácí tekutina kinetickou energii a aby protekla kanálem požadovanou rychlostí (průtokem), musí nabývat kinetickou energii na úkor tlakové energie – vzniká tlaková ztráta L_p, případně na úkor jiné energie, například potenciální energie apod.

Potrubí

Na Obrázku 1 je nejjednodušší případ vzniku tlakové ztráty při proudění nestlačitelné tekutiny v potrubí s konstantním průřezem. Protože na vstupu i výstupu z kanálu musí být stejný průtok, tedy i rychlost, bez změny potenciální energie, je tlaková ztráta L_p rovna rozdílu statických tlaků mezi vstupem a výstupem, viz Rovnice 1(a).

1: Tření tekutiny v potrubí a jeho důsledky

A [m²] průtočný průřez; F [N] třecí síla působící mezi stěnou kanálu a tekutinou; l [m] vyšetřovaná délka kanálu; L_p [Pa] tlaková ztráta na vyšetřované délce potrubí (pressure losses); L_q [J·kg^-1] ztrátové teplo způsobené vnitřním třením tekutiny; p [Pa] tlak; ρ [kg·m^-3] hustota pracovní tekutiny. Index _i označuje vstup, index _e výstup. Odvození rovnic je provedeno v Příloze 4.

Ztrátové teplo

Ztrátové teplo L_q, které vzniká při tření zahřívá pracovní tekutinu. Ztrátové teplo pro případ Obrázku 1 odpovídá tlakové energii tlakové ztráty, viz Rovnice 1(b).

Třecí síla

Tekutina působí třecí silou F na kanál ve směru proudění. Třecí síla pro případ Obrázku 1 odpovídá součinu rozdílu tlaku mezi vstupem a výstupem z kanálu (tlakové ztrátě) a průtočné plochy kanálu, viz Rovnice 1(c).

Trysky

Difuzory

Mimo tlakové ztráty při dopravě tekutin potrubím vzniká tlaková ztráta i při dynamických dějích v kanálech určené pro transformaci tlakové a kinetické energie tekutiny jako jsou trysky, difuzory a lopatkové kanály lopatkových strojů.

Klíčová slovaKapitola: Popis vzniku tlakové ztráty a základních pojmů

1.4

Laminární proudění

Turbulentní proudění

Velikost tlakové ztráty je funkcí vlastností pracovní tekutiny, tvaru kanálu, kterým protéká a drsnosti ploch tohoto kanálu. Přičemž postup výpočtu tlakové ztráty ve vyšetřovaném kanále se odvíjí podle toho, jestli je v kanále laminární a nebo turbulentní proudění. To lze zjistit podle hodnoty Reynoldsova čísla pro daný případ, pro jehož výpočet je nutné znát střední rychlost tekutiny, charakteristický rozměr kanálu (v případě potrubí se jedná o průměr) a hodnotu kinematické viskozity. Jestliže je hodnota Reynoldsova čísla menší než je hodnota kritického Reynoldosova čísla, pak bude proudění spíše laminární, jestliže je hodnota Reynoldsova čísla menší než je hodnota horního kritického Reynoldosova čísla, pak bude proudění pravděpodobně turbulentní.

Tlakovou ztrátu potrubní sítě stanovujeme proto, abychom dokázali stanovit tlak na konci potrubí a práci čerpadla či ventilátoru pro pokrytí energetických potřeb vzniku ztrátového tepla. Výpočet ztrátové tepla je důležitý i v kryogenice při dopravě zkapalněných plynů potrubím, protože ztrátové teplo tyto podchlazené tekutiny zahřívá a ty mohou ztrácet vlastnosti nebo se dokonce odpařovat.

Darcy-Weisbachova rovnice pro výpočet tlakové ztráty v potrubí

Henry Darcy

Julius Weisbach

Ztrátového součinitel

Potrubní tvarovky

Ventily

Z Navier-Stokesových rovnic lze snadno odvodit vztah pro výpočet tlakové ztráty pro případ laminárního ustáleného proudění jako funkci dynamického tlaku. Tato rovnice se nazývá Darcy-Weisbachova rovnice, kterou sestavil francouzský inženýr Henrym Darcym (1803-1858) pro potrubí, viz Rovnice 2. Později, na základě dlouhodobých experimentů a dedukce, potvrdil platnost tohoto vztahu německý inženýr Julius Weisbach (1806-1871) i pro proudění přechodové a turbulentní a dokonce i pro ztrátu v potrubních tvarovkách a ventilech. Použítí thoto vzorce je podmíněno předpokladem, že na vyšetřovaném úseku potrubí se nemění hustota. Nicméně při dopravě plynů na velmi dlouhých trasách plynovodů se může hustota měnit. Při přepravě plynů plynovody se řeší výpočet tlakové ztráty po úsecích, na kterých se vychází ze střední hustoty plynu na daném úseku.

2: Darcy-Weisbachova rovnice pro výpočet tlakové ztráty

ζ [1] ztrátový součinitel prvku vztažený ke kinetické energii střední rychlosti (definovaný Weisbachem); V‾ [m·s^-1] střední rychlost hmotnostního toku (střední rychlost proudění).

Klíčová slovaKapitola: Darcy-Weisbachova rovnice pro výpočet tlakové ztráty v potrubí

1.5

Z Darcy-Weisbachovy rovnice tedy plyne, že tlaková ztráta je určitým podílem z dynamického tlaku, tento podíl se nazývá ztrátový součinitel. Pro kanály stálého průřezu, respektive potrubí, lze ztrátový součinitel docela dobře vypočítat podle rovnic uvedených v kapitole Výpočet ztrátového součinitele potrubí. Pro jiné typy kanálů, například kolena, ventily apod. se používají výsledky z měření, viz kapitola Tlaková ztráta v místních odporech.

Výpočet ztrátového součinitele potrubí

Součinitel tření

Ztrátový součinitel potrubí neměnného průřezu lze vypočítat podle Rovnice 3. Je tedy funkcí délky a průměru potrubí (za d se dosazuje charakteristický rozměr, jestliže je potrubí nekruhového průřezu) a veličiny zvané součinitel tření, který lze v případě turbulentního proudění vypočítat pomocí.

3: Rovnice pro výpočet ztrátového součinitele potrubí

d [m] vnitřní průměr potrubí; l [m] délka potrubí; λ [1] součinitel tření v potrubí na vyšetřovaném úseku potrubí.

Součinitel tření

Johann Nikuradse

Nikuradseho diagram

Relativní drsnost

Hydraulicky hladké potrubí

Hydraulicky drsné potrubí

Nikuradse, 1933

Schiller, 1930

Moody, 1944

Rovnici součinitele tření v potrubí při laminárním proudění λ_LF lze snadno odvodit z Navier-Stokesových rovnic, viz Rovnice 4. Při určování hodnoty součinitele tření při turbulentním proudění se vychází ze závěru měření na sérii skleněných potrubí s uměle vytvořenou drsností pomocí pískového filmu, které provedl Johann Nikuradse. Nikuradse měřil tlakovou ztrátu několika potrubí s různými relativními drsnostmi povrchu pro vybraná Reynoldsova čísla a odtud vypočítal hodnoty součinitele tření λ podle Darcy-Weisbachovy rovnice (Rovnice 2). Z těchto hodnot vytvořil diagram závislosti součinitele tření na Reynoldsově čísle a potvrdil existenci čtyř oblastí s různými závislostmi součinitele tření na Reynoldsově čísle, viz Obrázek 4.

4: Nikuradseho diagram

Klíčová slovaKapitola: Výpočet ztrátového součinitele potrubí

1.6

vlevo-praktické rozdělení Nikuradseho diagramu; vpravo-originál Nikuradseho diagramu [Nikuradse, 1933]. (A) oblast laminárního proudění – lineární závislost součinitele tření; (B) přechodová oblast proudění z laminárního na turbulentní – může se vyskytovat jak laminární tak turbulentní proud; (C) turbulentní oblast proudění, ve které je součinitel tření funkcí Reynoldsových čísel i relativní drsnosti potrubí; (D) turbulentní oblast, ve které je součinitel tření funkcí prakticky pouze relativní drsnosti potrubí, tj. čím vyšší relativní drsnost, tím větší součinitel tření. C [1] relativní drsnost potrubí, viz také Nomogram 8; Re [1] Reynoldsovo číslo; Re_C [1] kritické Reynoldsovo číslo; λ_LF [1] součinitel tření při laminárním proudění (laminar flow), odvození rovnice je v Příloze 5; λ_SP [1] součinitel tření pro turbulentní proudění v hydraulicky hladkých potrubí (smooth-pipe, C→0) [Schiller, 1930] ; λ_RP [1] hranice, od které se se zvyšujícím se Reynoldsovým číslem součinitel tření nemění, tzv. proudění v hydraulicky drsném potrubí (rough pipe) [Moody, 1944]; ε [m] absolutní drsnost vnitřních stěn potrubí (hodnoty například viz. Tabulka 7).

Součinitel tření

Turbulentní proudění

Colebrookova rovnice

Cyril Colebrook

Lewis Moody

Moodyho diagram

Moody, 1944

K výpočtu součinitele tření v oblastech (C)+(D) na Obrázku 4 se používají poloempirické vztahy získané aproximací skutečně naměřených hodnot v Nikuradseho diagramu doplněného o další měření, která byla provedena. Existuje jedna univerzální rovnice s dostatečnou přesností pro běžnou technickou praxi, kterou sestavil Cyril Colebrook (1910-1997), viz Rovnice 5. Americký inženýr Lewis Moody (1880-1954) pak vytvořil pomocí Colerbrookovy rovnice diagram vypočítaných hodnot součinitele tření, který se dnes označuje jako Moodyho diagram. Moodyho diagram je široce publikován on-line i knižně, například [Moody, 1944].

5: Colebrookova rovnice pro výpočet součinitele tření potrubí

Mezní Reynoldsovo číslo

V oblasti (C) probíhá vývoj turbulentního rychlostního profilu. V oblasti (D) je již vývoj dokončen a i při zvyšující se hodnotě Reynoldsova čísla se podíl kinetické energie tekutiny v mezní vrstvě ku kinetické energie v jádru proudu nemění. Hodnoty mezních Reynoldsových čísel Re_RP, tedy přibližnou hranici mezi oblastmi (C) a (D) lze vypočítat dosazením rovnice pro λ_RP do Colebrookovy rovnice. Vybrané hodnoty takto vypočítaných mezních Reynoldsových čísel jsou uvedeny v Tabulce 6.

	C	1·10^-6	1·10^-5	1·10^-4	0,001	0,01	0,01	0,04	0,05
	Re_RP	2,62·10⁹	2,22·10⁸	1,82·10⁷	1,42·10⁶	2,28·10⁵	1,02·10⁵	1,95·10⁴	1,48·10⁴

6: Orientační hodnoty mezního Reynoldsova čísla

C [1]; Re_RP [1] mezní Reynoldsovo číslo, při kterém přestává být součinitel tření citlivý na změnu Re

Klíčová slovaKapitola: Výpočet ztrátového součinitele potrubí

1.7

	ε		ε
Tažené (nové) z: měď, mosaz, sklo	0 - 0,0015	Litinové	0,26 - 1
Plast	≤0,0015	Ocelové pozinkované	0,15
Ocelové bezešvé válcované	0,04 - 0,1	Ocelové trubky korodované vyčištěné	0,15...0,2
Ocelové svařované podélným švem	0,05...0,1

7: Orientační hodnoty absolutních drsností trubek

[mm]. Výběr z [Stephan et al., 2010, p. 1058].

8: Nomogram pro výpočet relativní drsnosti

d [mm], ε [mm], C [1].

Plynovod

Z Darcy-Weisbachovy rovnice plyne, že pro minimální tlakovou ztrátu je výhodné přepravovat plyn při vyšších tlacích a hustotách než při nízkých tlacích a vysokých rychlostech. Proto jsou tlaky v tranzitních plynovodech kolem 7 MPa a tlak plynu se snižuje před spotřebiči (viz Tabulka 9), které jsou kvůli bezpečnosti konstruovány na nižší tlaky.

	p		p
Tranzitní plynovod	7,5	Středotlaký plynovod	0,1...0,3
Vysokotlaký plynovod	4	Nízkotlaký (domácnosti)	0,002

9: Přetlaky v plynovodech zemního plynu

p [MPa] přetlak v plynovodu.

Měrná tlaková ztráta v potrubí

Pro základní návrhy potrubní trasy využívají projektanti veličinu měrná tlaková ztráta v potrubí odpovídající tlakové ztrátě v potrubí o délce 1 m, viz také Nomogram 10.

Klíčová slovaKapitola: Měrná tlaková ztráta v potrubí

1.8

10: Nomogram pro výpočet měrné tlakové ztráty, dynamického tlaku a měrné kinetické energie tekutiny v potrubí

p_d [Pa] střední dynamický tlak proudu; d [mm], Q [m³·s^-1], V‾ [m·s^-1], ρ [kg·m^-3], λ [1], π_L [Pa·m^-1] měrná tlaková ztráta.

Tlaková ztráta v místních odporech

Potrubní trasa/síť

Potrubní trasa (potrubní síť) nebývá přímočará a může být tvořena dalšími potrubními prvky (odbočky různých tvarů, oblouky, zúžení), armaturami, filtry, měřidly a dalšími průtočnými částmi, viz Obrázek 11. Tyto prvky jsou místními odpory a vzniká v nich místní tlaková ztráta.

Klíčová slovaKapitola: Tlaková ztráta v místních odporech

1.9

11: Příklad potrubní trasy s vyznačením místních odporů

a-šoupátko; b-uzavírací ventil (obecně má vyšší tlakovou ztrátu než šoupátko); c-odbočka (T-kus); d-plynulé zúžení; e-oblouk (koleno).

Škrcení

Tlakové ztráty v místních odporech bývají mnohem intenzivnější než v rovném úseku potrubí vzhledem k tomu, že při průtoku těmito částmi dochází i ke změně tvaru průtočného kanálu, směru proudění a často i ke škrcení tekutiny. Za speciální případ místního odporu, lze považovat i vstupy a výstupy z trubky. Na okrajích je totiž proudění většinou neustálené a ovlivněné tvarem začátku či konce potrubí.

Střední rychlost

Tlakovou ztrátu místního odporu lze vypočítat také podle Rovnice 2, přičemž za střední rychlost se dosazuje střední rychlost proudu před prvkem.

Ztrátový součinitel

Stephan et al., 2010

Ztrátový součinitel ζ některých typů místních odporů lze i vypočítat, častěji se ale vychází z měření daného místního odporu pro různá Reynoldsova čísla. Nicméně u některých typů místních odporů není vliv Reynoldsova čísla významný a lze použít tabelizované hodnoty, především pro armatury a potrubní tvarovky např. v [Stephan et al., 2010, s. 1065]. Příslušný ztrátový součinitel poskytuje výrobce daného potrubního prvku.

Klíčová slovaKapitola: Tlaková ztráta v místních odporech

1.10

Ztrátový součinitel

Armatura

Stephan et al., 2010

V případě armatury (ventily, šoupátka apod.) obvykle výrobce také dodává přímo grafy závislosti její tlakové ztráty na průtoku (podle druhu protékajícího média). Pokud je znám jmenovitý průtokový součinitel armatury K_VS, lze ztrátu v závislosti na průtoku vypočítat pomocí Rovnice 12. Jmenovitý průtokový součinitel se měří na úseku 2·d před armaturou a 8·d za armaturou, proto takto vypočítaný ztrátový součinitel zahrnuje i tuto délku potrubí. Takže skutečný ztrátový součinitel armatury je nižší o ztrátový součinitel odpovídající 10·d hladkého potrubí. Orientační hodnoty ztrátových součinitelů některých armatur jsou uvedeny v [Stephan et al., 2010, s. 1073]. Existují ale i jiné typy součinitelů zpravidla odvozené od tlakové ztráty armatury. Záleží na výrobci jakou metodiku porovnávání armatur používá. Příslušné vztahy potom uvádí ve svém katalogu armatur.

12: Výpočet ztrátového součinitele armatury

d [mm] vnitřní průměr vstupu a výstupu armatury; K_VS [m³·h^-1] jmenovitý průtokový součinitel armatury. Vztah je odvozen pro průtok vody v [Roček, 2002, s. 236].

Uzavírací ventil

Při výběru velikosti nejvhodnější uzavírací armatury se nejdříve stanoví povolená tlaková ztráta L_p při objemovém průtoku Q a hustotě proudícího média na vstupu ρ. Vypočítá se jmenovitý průtokový součinitel K_VS. Dále se z katalogu armatur příslušného výrobce vybere armatura s nejbližším vyšším K_VS.

Ekvivalentní délka potrubí

Fraas, 1989

Pro přibližný výpočet tlakové ztráty místního odporu lze použít i veličinu zvanou ekvivalentní délka potrubí. Tato veličiny udává délku hladkého potrubí (vyjádřená jako počet průměrů hladkého potrubí) o stejném průměru jako je vstupní průměr vyšetřovaného místního odporu se stejnou tlakovou ztrátou. Ekvivalentní délky potrubí některých armatur a potrubních tvarovek jsou uvedeny v [Fraas, 1989, s. 447], výběr pak v Tabulce 13. Výhodou je, že při výpočtu stačí jednotlivé ekvivalentní délky sečíst a vypočítat jejich celkovou tlakovou ztrátu jako by se jednalo o stejně dlouhé hydraulicky hladké potrubí, viz Úloha 1.

	l·d^-1		l·d^-1
VENTILY PŘÍMÉ
obyčejné	340	s šikmým vedení vřetena 60° od osy potrubí	175

Klíčová slovaKapitola: Tlaková ztráta v místních odporech

1.11

	l·d^-1		l·d^-1
s vedením vřetena i v průtočné části	450	s šikmým vedení vřetena 45° od osy potrubí	145
NÁROŽNÍ VENTILY
obyčejné	145	s vedením vřetena i v průtočné části	200
ŠOUPÁTKA
obyčejné (dvě sedla)	13	pro plynovody	3
pro velmi vazké kapaliny (jedno sedlo)	17
ZPĚTNÉ VENTILY
se zpětnou klapkou	35	s kuličkou	150
s plně otvíratelnou klapkou	50	se sacím košem deskový	420
přímé	340	se sacím košem s klapkou	75
nárožní	145	uzavírací klapky	20
KOHOUTY
obyčejné	18	třícestné	140
POTRUBNÍ TVAROVKY
90° koleno	30	rohové koleno (bez radiusu)	57
45° koleno	16	180° koleno (malé)	50
90° koleno (velký rádius)	20	tvarovka T	20
90° koleno s hrdlem (k pájení nebo šroubení)	50	tvarovka T (většina průtoku odbočuje do větve)	60
45° koleno s hrdlem (k pájení nebo šroubení)	26
PRŮTOKOMĚRY
turbínový	150	clonkový	200
pístový (objemový)	400

13: Ekvivalentní délka potrubí l·d^-1 některých armatur a potrubních tvarovek

l·d^-1 [1] ekvivalentní délka potrubí. Výběr z [Fraas, 1989], doplněno o průtokoměry [Izard, 1961, s. 299].

Zde můžete vyzkoušet aplikaci společnosti viklan.cz:

Hospodárná rychlost proudění

Pořizovací náklady

Provozní náklady

Stephan et al., 2010

Z Darcyho-Weisbachovy rovnice vyplývá, že vyšší střední rychlost způsobuje vyšší tlakovou ztrátu. S rostoucí tlakovou ztrátou stoupá cena pracovního stroje (čerpadla, ventilátoru...) a provozní náklady. Větší průměr potrubí snižuje rychlost proudění, ale zvyšuje náklady na pořízení potrubních tras a armatur. Hodnoty hospodárných rychlostí pro různé látky lze nalézt v [Stephan et al., 2010, p. 1063], v Tabulce 14 je výběr. Existují však i jiné důvody pro nižší/vyšší rychlosti než je hospodárnost, např. dispoziční důvody apod.

Klíčová slovaKapitola: Hospodárná rychlost proudění

1.12

	V‾		V‾
Olej	1...2	Pára přehřátá do 4 MPa	20...40
Voda	1...4	Pára přehřátá o vysokém tlaku	30...60, 80
Pára topná o nízkém tlaku	10...15	Výfuková pára (po expanzi ve stroji)	15...30
Pára sytá do 1 MPa	15...20	Vzduch (stlačený)	2...4

14: Hodnoty hospodárných rychlostí v potrubí

V‾ [m·s^-1]

Průměr potrubí

Z navržené hospodárné rychlosti proudění, hustoty a požadovaného měrného průtoku se vypočítá průměr potrubí d, viz Nomogram 15. Vypočítaný průměr potrubí je nutné zaokrouhlit podle vyráběných průměrů trubek odpovídající tlaku a teplotě, při které bude potrubí provozováno.

15: Nomogram pro výpočet průměru potrubí

V‾ [m·s^-1], ρ [kg·m^-3], m^• [kg·s^-1] hmotnostní tok; m^•_m [kg·min^-1], m^•_h [kg·h^-1], Q [m³·s^-1] objemový tok; Q_m [m³·min^-1], Q_h [m³·h^-1] objemový průtok potrubím, d [mm] průměr potrubí.

Klíčová slovaKapitola: Charakteristika potrubního systému

1.13

Charakteristika potrubního systému

Závislost tlakové ztráty potrubní trasy na objemovém průtoku se nazývá charakteristika potrubního systému. Z rovnice pro výpočet tlakové ztráty je zřejmé, že při ρ=konst. bude tlaková ztráta kvadratickou funkcí s parametrem C_S zvaným konstanta potrubního systému (jiný název měrný hydraulický odpor potrubní trasy), viz Rovnice 16.

16: Charakteristika potrubního systému

n [-] počet jednotlivých úseků potrubí (každý úsek má po celé délce konstantní průměr); k [-] počet místních odporů; L_pipe [Pa] tlaková ztráta při proudění daným úsekem potrubního systému; L_component [Pa] tlaková ztráta místního odporu; C_S [kg·m^-7] konstanta potrubního systému; Q [m³·s^-1] objemový průtok. L_p,n [Pa] tlaková ztráta při jmenovitém průtoku Q_n systémem. Rovnice platí i pro potrubí nekruhového průřezu.

Konstanta potrubního systému

Konstanta potrubního systému C_S se většinou uvažuje jako konstanta pro dané otevření jednotlivých armatur, ale protože součinitel tření λ je funkcí Reynoldsova čísla, musí se s průtokem měnit i C_S. Tato změna není ovšem příliš velká pokud nás zajímá tlaková ztráta v oblasti jmenovitého průtoku. Konstanta potrubního systému C_S se také mění otevíraním/zavíráním ventilů (změna jejich tlakové ztráty), proto se někdy uvádní několik křivek charakteristik potrubního systému pro jednotlivé polohy vřeten ventilů.

Konstantu potrubního systému lze vypočítat podle Rovnice 16 z jednotlivých tlakových ztrát potrubního systému pro známý (jmenovitý) průtok (viz Úloha 1) a nebo ji lze vypočítat z naměřené tlakové ztráty při konkrétním objemovém průtoku, viz Úloha 2.

Klíčová slovaKapitola: Určení charakteristiky potrubního systému z měření

1.14

Určení charakteristiky potrubního systému z měření

Logaritmická soustava souřadnic

Potrubní charakteristiku L_p=f(Q) lze zjistit měřením pro několik případů. Následně lze toto měření zpracovat na počítači pomocí připraveného softwaru. Ručně lze rovnici určit zakreslením naměřených dat v logaritmické soustavě souřadnic a tato data proložit přímkou jejíž směrnice, podle pravidel logaritmického počtu, odpovídá mocnině průtoku, viz Úloha 2.

Změna tlakové ztráty při znečištění a korozi potrubí

Znečišťování a koroze potrubí a výměníků obvykle postupně způsobuje takové problémy, že je nutné je vyčistit (zvýšení tlaku v potrubním systému a vznik netěsností, zvýšení čerpací práce apod.).

Znečištění potrubí

Ke znečištění potrubí může dojít, jestliže kapalina není čistá. Na Obrázku 17 je uvedena změna tlakové ztráty v potrubí při rovnoměrném nánosu v potrubí – o stejná procenta zvýšení tlakové ztráty se přibližně zvýší i čerpací práce. Závislost na tomto obrázku byla vytvořena dosazením Darcy-Weisbachovy rovnice do podílu tlakové ztráty L_p po zúžení průtočného průřezu a tlakové ztráty L_p,n. Odtud je patrné, že vliv zúžení na tlakovou ztrátu roste s pátou mocninou. Naproti tomu i při zachování absolutní drsnosti je vliv změny součinitele tření o několik řádů nižší.

17: Změna tlakové ztráty potrubí při znečištění

Vytvořeno pro d_n=100 mm; V_n=3 m·s^-1; ε_n=0,05 mm; υ_n=553,2 nm²·s^-1 (voda při teplotě 50 °C); Q=konst. F-nános v potrubí (fouling). Index _n označuje parametry před znečištěním potrubí.

Klíčová slovaKapitola: Změna tlakové ztráty při znečištění a korozi potrubí

1.15

Krystalizace minerálů

Biologické znečištění

Znečištění tuhými částicemi

Ke znečištění potrubí může dojít důsledkem chemického nebo biologického působení a nebo obsahem tuhých částic v kapalině. V případě chemického či elektrochemického procesu dochází k vysrážení minerálů a jejich krystalizace na vnitřní plochách potrubí. Biologická usazenina na potrubí může být rostlinného i živočišného původu – většinou se jedná o nějaké druhy řas nebo korýšů a velmi zavísí na teplotě vody, obsahu živin ve vodě a v případě řas i světelných podmínkách. Typickým znakem znečištění potrubní trasy tuhými nečistotami v kapalině je, že není rovnoměrně rozložená po celé délce potrubí. Tuhé částice se usazují v místech s malou rychlostí proudění, v nejnižších bodech potrubní trasy odkud je proud kapaliny není schopen vytlačit a před zúženími.

Mezní rychlost

Pugh et al., 2009

K usazování vodního kamene na stěny potrubí nedochází přibližně již při mezních rychlostech 1,5 až 2,5 m·s^-1. Nicméně při určitych kombinacích pH a teplot tato rychlost nemusí stačit. Usazování tuhých částic lze zamezit usazovaní mechanických nečistot už od rychlostí kolem 1,5 m·s^-1, ale také záleží i na orientaci potrubí a velikosti a hmotnosti jednotlivých částic. Biologickému znečištění potrubí lze zabránit při rychlostech nad 2 m·s^-1. Uvedené mezní rychlosti rychlosti znášení jsou pro vodu a údaje o nich pochází z [Pugh et al., 2009]. U jiných kapalin se mezní rychlost může lišit, protože zamezení přilnutí nečistot k povrchu trubky je potřebné určité tečné napětí, které je funkcí viskozity, takže kapaliny s vyšší viskozitou zamezí znečištění při nižších rychlostech a obráceně. Stálou (mezní) rychlost proudění při nepravidleném provozu potrubí lze udržet vytvořením smyček na ohrožených částech potrubí, ve kterých bude proudit kapalina stálou rychlostí bez ohledu na průtok mezi vtokem a výtokem z potrubí.

Klíčová slovaKapitola: Změna tlakové ztráty při znečištění a korozi potrubí

1.16

Odstávka potrubí

Období, kdy bude nutné potrubí vyčistit, tedy dobu odstávky, lze predikovat pomocí statistiky. Tato statistická metoda je založena na předpokladu, že nárůst tlakové ztráty se řídí Rayleighovým rozdělením pravděpodobnosti, viz Obrázek 18. Pro predikce zvýšení tlakové ztráty kvůli znečištění potrubí stačí znát odhad doby provozu, po které se tlaková ztráta začne zvyšovat, očekávaný modus rychlosti, při které roste tlaková ztráta nejrychleji a také rychlost nárůstu tlakové ztráty na počátku usazování nečistot, viz Úloha 379. Tyto odhady lze při reálném provozu zpřesňovat pomocí měření tlakové ztráty a tak zpřesňovat i predikce nárůstu tlakové ztráty v čase.

18: Rayleighovo rozdělení aplikované na změnu tlakové ztráty

n [s^-1] změna tlakové ztráty v čase; t [s] čas. Vodorovná osa označuje rozdíl (V-V_n), protože Rayleighovu rozdělení pravděpodobnosti začíná v nule a nánosy se tvoří až po nějaké době, kdy rychlost proudění je nominální V_n. Index _n označuje parametry před usazováním nečistot v potrubí.

Koroze potrubí

Koroze potrubí zvyšuje absolutní drsnost potrubí současně způsobuje úbytek tloušťky stěn potrubí. Jestliže úbýtek materiálu nezpůsobuje významnou změnu protočné plochy potrubí, pak, při konstatních hodnotách ostatních parametrů v Darcyho-Weisbachovy rovnice, lze podíl tlakové ztráty L_p ku tlakové ztrátě při jmenovité (počáteční) L_p,n vyjádřit jako podíl součinitelů tření. Z dat Tabulky 7 je patrné, že koroze může zvětšit tlakovou ztrátu řádově o desítky procent. Při výpočtu potrubí, které nebude čištěno od koroze je tedy nutné počítat tlakovou ztrátu jako by potrubí bylo zkorodované.

Klíčová slovaKapitola: Tlaková ztráta při významné změně hustoty

1.17

Tlaková ztráta při významné změně hustoty

Fannovy rovnice

Dejč, 1967

Zucker and Biblarz, 2002

Mimo dopravy tekutin se setkáváme s dynamickým proudem plynů, při kterém se může významně měnit hustota plynu. Jestliže se jedná o adiabatické proudění plynu kanálem konstatního průřezu, pak lze vycházet při stanovení tlakové ztráty z toho, že celková entalpie plynu zůstává konstantní a rovna celkové entalpii na vstupu do kanálu, ale bude se zvyšovat entropie v důsledku vnitřního tření. Na tomto předpokladu lze odvodit tzv. Fannovu Rovnici 19.

19: Rovnice pro výpočet tlakové ztráty při proudění plynu kanálem s konstantní průtočnou plochou (Fannovy rovnice)

V^*_i [m·s^-1] kritická rychlost pro případ izoentropického proudění; κ [1] poměr teplených kapacit; A [m²] průtočný průřez kanálu; V [m·s^-1] rychlost plynu ve vyšetřovaném místě kanálu (tato rychlost odpovídá rychlosti při izoentropické expanzi z celkového tlaku p_s do tlaku statického p); G=konst. Jestliže kanál není kruhový použije se místo d charakteristický rozměr L jako při nestlačitelném proudění. Odvození v [Dejč, 1967, s. 209], [Zucker and Biblarz, 2002, s. 283].

Součinitel tření

Dejč, 1967

Součinitel tření λ v Rovnicích 19 je konstantní po celé délce kanálu, ale ve skutečnosti je více či méně závislý na Re a Machovu číslu ve vyšetřovaném místě kanálu. Experimentální ověření změn součinitele tření při stlačitelné proudění a platnosti Rovnic 19 je provedeno v [Dejč, 1967, s. 217].

Fannovy křivky

Při adiabatickém proudění plynu se plyn zahřívá v důsledku tření, což způsobuje zvětšování jeho měrného objemu a tedy i rychlosti v kanále konstantní průtočné plochy. To znamená, že postupně v plynu klesá tlak a měrná entalpie. Zakreslení stavů plynu v jednotlivých bodech osy kanálu v h-s diagramu označujeme jako Fannovu křivku (Fanno line). Na Obrázku 20 jsou tři Fannovy křivky pro kanál délky l a různé velikosti součinitele tření λ (stejný vliv jako změny součinitele tření má na změnu tlaku i prodlužování kanálu). Při maximálním součiniteli tření λ₁ nedosáhne proudění na výstupu z kanálu kritické rychlosti, λ₂ je takový, aby proudění na výstupu dosáhlo právě kritické rychlosti. Součinitel λ₃ je menší jak λ₂ a přesto proudění dosáhne na výstupu také jen kritické rychlosti.

Klíčová slovaKapitola: Tlaková ztráta při významné změně hustoty

1.18

20: Fannovy křivky

h [J·kg^-1] entalpie; s [J·kg^-1·K^-1] entropie; h_s [J·kg^-1] celková entalpie plynu; h* [J·kg^-1] kritická entalpie; p_sur [Pa] tlak okolí na výstupu z kanálu (surrounding). Index _i označuje počáteční stav plynu, index _e konečný stav plynu (na konci úseku/sledovaného děje). Dolní index _s označuje celkový stav plynu.

Ucpávky

Součinitel tření

V technické praxi je uvedená teorie uplatnitelná zejména při vyšetřovaní proudění v bezdotykových ucpávkách. Na vysoké tlakové ztrátě spojené s prouděním plynu ve velmi malé mezeře je také založen princip suchoběžných plynových ucpávek. Nicméně i labyrintové ucpávky lze připodobnit k hladké ucpávce s konstantním průtočným průřezem a s konkrétním součinitelem tření.

Úlohy

Úloha 1:

Určete charakteristiku potrubního systému na výtlaku kondenzátního čerpadla (viz přiložený obrázek), ve kterém je kondenzát čerpán z pomocné nádrže kondenzátu CT1 do napájecí nádrže přes ohřívák kondenzátu H1. Na trasu je napojen paralelní potrubní systém se záložním čerpadlem (modrá barva). Teplota vody na výstupu z čerpadla je 60 °C a za ohřívákem H1 105 °C. Průtok čerpadlem je 2,4 m³·h^-1. Průtokový součinitel kulového kohoutu 001 je 48,5 m³·h^-1. Zpětný ventil má tlakovou ztrátu 5 kPa. Minimální tlaková ztráta vyvažovací armatury je 750 Pa. Tlaková ztráta vodoměru je 18 kPa. Tlaková ztráta ohříváku H1 je 12 kPa. Potrubí je běžné vodovodní jednopalcové. Řešení úlohy je uvedeno v Příloze 1.

Klíčová slovaKapitola: Úlohy

1.19

CT1-pomocná nádrž kondenzátu č. 1 (condenser tank); H1-ohřívák č. 1 (heater); WM1-vodoměr č. 1 (water meter); valve number-číslo armatury; engine number-číslo motoru. Délky jednotlivých úseků potrubního systému jsou uvedeny v metrech.

§1

zadání:

t_i; t_e; Q_n; K_VS,001; L_p,002; L_p,003; L_p,WM1; L_p,H1; l

§6

výpočet:

ζ_pipe; L_pipe

§2

odečet:

ν; ρ

§7

výpočet:

L_p,001

§3

odečet:

d; ε

§8

výpočet:

L_p,elbow

§4

výpočet:

V¯; Re

§9

výpočet:

L_{p, n}; C_S

§5

výpočet:

Popisek symbolů je v Příloze 1.

Úloha 2:

Nalezněte přibližnou hodnotu konstanty potrubního systému určeného pro vytápění. Potrubím proudí tepla voda. K dispozici jsou naměřené průtoky systémem a příslušná tlaková ztráta uvedené v tabulce níže. Naměřené hodnoty upraveny z [Pleskot, 1947, s. 17]. Řešení úlohy je uvedeno v Příloze 2.

	L_p	10	25,1	62	140	320	700	1400
	Q	19,64	29,64	50,07	74,61	113,9	161	233,7

Tabulka naměřených hodnot

Hodnoty naměřené tlakové ztráty v potrubí zakreslené na logaritmickém papíře

L_p [Pa], Q [m³·s^-1].

Klíčová slovaKapitola: Úlohy

1.20

§1

zadání:

L_p; Q

§4

odečet:

x; P

§2

vyznačení:

L_p; Q do grafu

§5

výpočet:

C_S

§3

aproximace:

hodnot L_p; Q přímkou

Popisek symbolů je v Příloze 2.

Úloha 3:

Navrhněte očekávané zvýšení tlakové ztráty deskového výměníku voda/voda pomocí statistické metody. Ve výměníku krystalizuje vodní kámen. Jmenovitá rychlost proudění ve výměníku je 1 m·s^-1 a jmenovitá tlaková ztráta je 0,185 bar. Na základě zkušeností s provozem předchozích výměníků očekáváme, že tlaková ztráta začne narůstat již po 500 minutách s počáteční rychlostí 0,2703·10^-3 min^-1, přičemž parametry (V-V_n)-n křivky z Obrázku 18 jsou: n_max=2,1622·10^-3min^-1; (V-V_n)_mod=1,1911 m·s^-1. Při provozu zůstává průtok konstantní. Řešení úlohy je uvedeno v Příloze 3.

Zvýšení tlakové ztráty ve výměníku kvůli jeho znečištění

L_p [bar]; t [min] čas.

§1

zadání:

V_n; L_p,n; t₀; n₀; n_max; (V-V_n)_mod

výpočet:

Δt

§2

výpočet:

§4

výpočet:

(L_p/L_p,n)_k=1; V_k=1; L_{p, k=1}

§3

návrh:

t_max; k_max

§5

výpočet:

V_k; n_k; (L_p/L_p,n)_k; L_{p, k}

Popisek symbolů je v Příloze 3.

Odkazy

ŠKORPÍK, Jiří, 2022b, Základní rovnice lopatkových strojů, Transformační technologie, Brno, ISSN 1804-8293, https://turbomachinery.education/zakladni-rovnice-lopatkovych-stroju.html.

DEJČ, Michail, 1967, Technická dynamika plynů, SNTL, Praha.

FRAAS, Arthur, 1989, Heat exchanger design, John Wiley&Sons, Inc., ISBN 0-471-62868-9.

IZARD, Julien, 1961, Příručka technické fyziky, Státní nakladatelství technické literatury, Praha.

MOODY, Lewis, 1944, Transactions of the ASME, Friction factors for pipe flow, 66 (8). http://www.ipt.ntnu.no/~asheim/TPG4135/Moody.pdf

NIKURADSE, Johann, 1933, Strömungsgesetze in rauhen rohren, V. D. I. Forschungsheft, 361: 1–22, Berlin.

PLESKOT, Václav, 1947, Nomografie v technické praxi, Praha, SPASEI.

PUGH, Simon, HEWITT, Geoffrey, MÜLLER-STEINHAGEN, Hans, 2009, Fouling During the Use of “Fresh” Water as Coolant—The Development of a “User Guide”, Heat Transfer Engineering, 30:10-11, 851-858, DOI: 10.1080/01457630902753706.

ROČEK, Jaroslav, 2002, Průmyslové armatury, INFORMATORIUM, Praha, ISBN 80-7333-000-8.

VZNIK TLAKOVÉ ZTRÁTY PŘI PROUDĚNÍ TEKUTINY A JEJÍ VÝPOČET

Popis vzniku tlakové ztráty a základních pojmů

Vnitřní tření

Potrubí

Ztrátové teplo

Třecí síla

Trysky

Difuzory

Laminární proudění

Turbulentní proudění

Darcy-Weisbachova rovnice pro výpočet tlakové ztráty v potrubí

Henry Darcy

Julius Weisbach

Ztrátového součinitel

Potrubní tvarovky

Ventily

Výpočet ztrátového součinitele potrubí

Součinitel tření

Součinitel tření

Johann Nikuradse

Nikuradseho diagram

Relativní drsnost

Hydraulicky hladké potrubí

Hydraulicky drsné potrubí

Součinitel tření

Turbulentní proudění

Colebrookova rovnice

Cyril Colebrook

Lewis Moody

Moodyho diagram

Mezní Reynoldsovo číslo

Plynovod

Měrná tlaková ztráta v potrubí

Tlaková ztráta v místních odporech

Potrubní trasa/síť

Škrcení

Střední rychlost

Ztrátový součinitel

Ztrátový součinitel

Armatura

Uzavírací ventil

Ekvivalentní délka potrubí

Hospodárná rychlost proudění

Pořizovací náklady

Provozní náklady

Průměr potrubí

Charakteristika potrubního systému

Konstanta potrubního systému

Určení charakteristiky potrubního systému z měření

Logaritmická soustava souřadnic

Změna tlakové ztráty při znečištění a korozi potrubí

Znečištění potrubí

Krystalizace minerálů

Biologické znečištění

Znečištění tuhými částicemi

Mezní rychlost

Odstávka potrubí

Koroze potrubí

Tlaková ztráta při významné změně hustoty

Fannovy rovnice

Součinitel tření

Fannovy křivky

Ucpávky

Součinitel tření

Úlohy

Odkazy