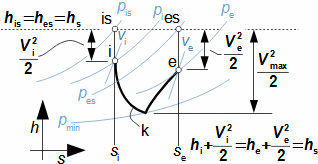
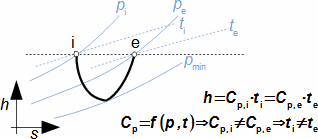
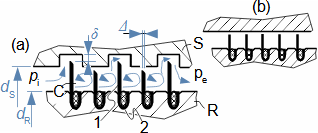
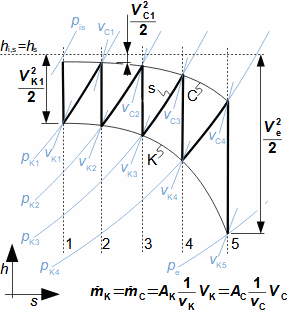
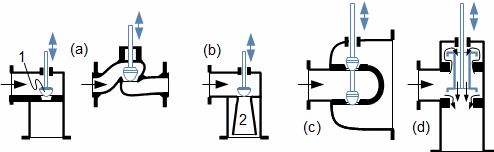
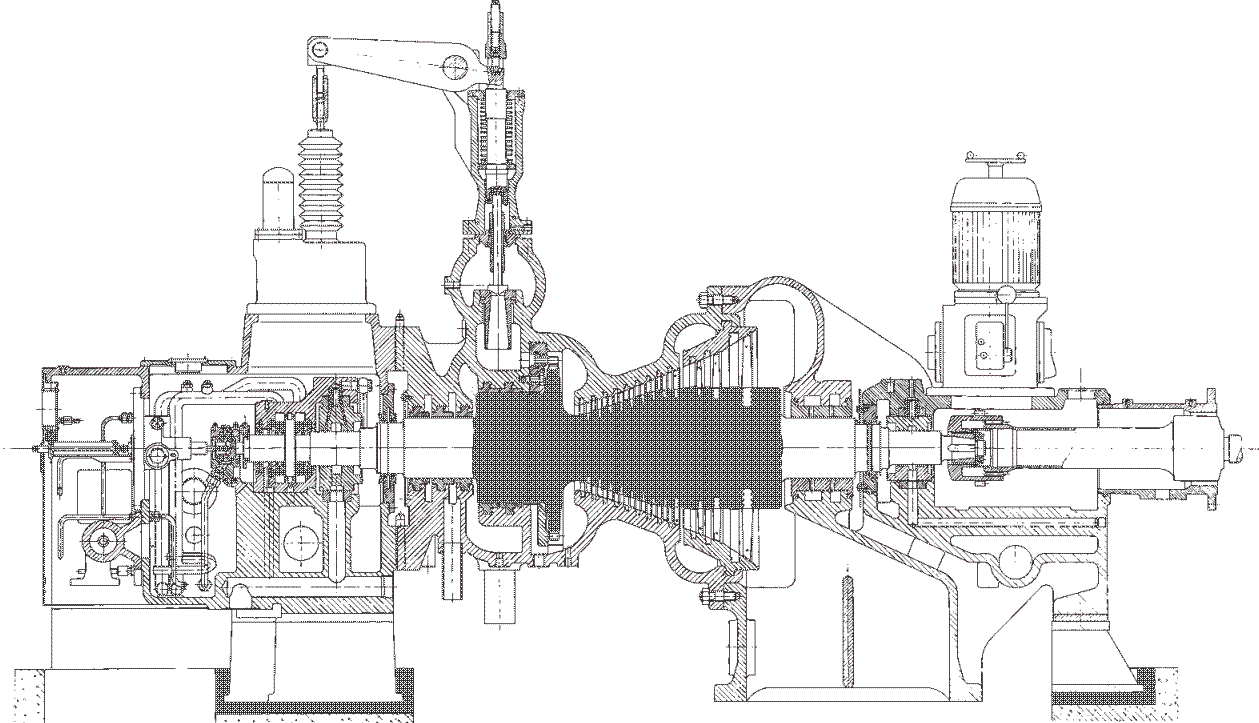
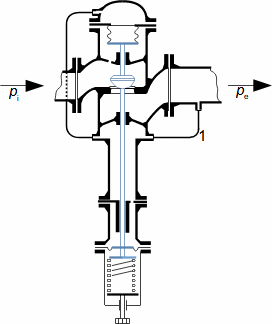
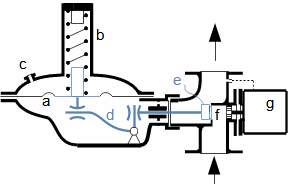
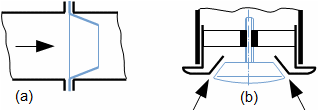
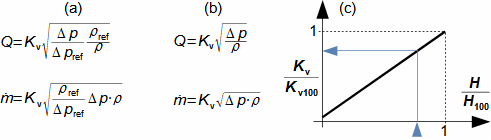fluid-dynamics.education
6.

ŠKRCENÍ PLYNŮ A PAR

6.3 . . . . . . . . . . . . . .
Škrcení jako termodynamická změna
6.3 . . . . . . . . . . . . . .
Popis vzniku tlakové ztráty a změn ostatních stavových veličin tekutiny při škrcení
● Mechanismus škrcení clonou ● Joulův-Thomsonův jev
6.5 . . . . . . . . . . . . . .
Využití efektu škrcení v labyrintových ucpávkách
● Ideální labyrintová ucpávka ● Konstrukce labyrintových ucpávek ● Propojení labyrintových ucpávek
6.8 . . . . . . . . . . . . . .
Regulační ventily
● Jednosedlové ventily ● Ventil s difuzorem ● Dvousedlové ventily ● Průtok ventilem
6.12 . . . . . . . . . . . . . .
Redukční ventily a redukční stanice
● Redukční ventily ● Redukční stanice
6.15 . . . . . . . . . . . . . .
Škrcení v průřezových průtokoměrech
6.16 . . . . . . . . . . . . . .
Hydraulické vyvažování potrubí pomocí škrcení
6.16 . . . . . . . . . . . . . .
Úloha 1: Výpočet kinetické energie, entalpie a celkové entalpie plynu
Úloha 2: Výpočet škrcení páry
Úloha 3: Výpočet labyrintové ucpávky
6.18 . . . . . . . . . . . . . .
Odkazy
6.19 - 6.24 . . . . . . . . . .
Přílohy
X . . . . . . . . . . . . . . .
Doplňkový mediální obsah
Zobrazení v PDF
fluid-dynamics.education 
6.2
autor:
ŠKORPÍK, Jiří – LinkedIn.com/in/jiri-skorpik
datum vydání:       
Leden 2006, červen 2023 (2. vydání)
název:
Škrcení plynů a par
web:
fluid-dynamics.education
provenience:
Brno (Česká republika)
email:
skorpik.jiri@email.cz

Copyright©Jiří Škorpík, 2023
Všechna práva vyhrazena.

Klíčová slovaŠKRCENÍ PLYNŮ A PAR
6.3

Škrcení jako termodynamická změna

Škrcení

Tlaková ztráta

Škrcení je termodynamický změna, při kterém dochází k trvalé tlakové ztrátě proudící tekutiny a nárůstu entropie. Tekutina při škrcení nekoná vnější práci – pouze dochází k disipaci energie.

Víry

O škrcení plynů a par hovoříme tehdy, dochází-li k tlakové ztrátě na velmi krátkém úseku v důsledku tvorby vírů, například v kanálu s prudkou změnou průtočného průřezu. Škrcení je  technické praxi častý jev, většinou se jedná o jevy nežádoucí, například ve ventilech, ale jsou i případy, ve kterých škrcení plní užitečnou funkci, např. se pomocí škrcení snižuje únik plynů v labyrintových ucpávkách nebo redukuje tlak plynu.

Popis vzniku tlakové ztráty a změn ostatních stavových veličin tekutiny při škrcení

Výsledkem škrcení je vždy tlaková ztráta, ale projevem škrcení jsou i změny teploty, která se může zvyšovat i snižovat, což je označováno jako Joulův-Thomsonův jev.

Mechanismus škrcení clonou

Koutové víry

Entropie

Vznik tlakové ztráty je dobře patrný při průtoku tekutiny clonou. Clona je náhlé zúžení průřezu potrubí (Obrázek 1), takže v ní dojde ke zvýšení rychlosti proudící tekutiny. S nárůstem rychlosti musí klesat tlak ze zákona zachování energie, u plynů dojde i k poklesu teploty. Před a za clonou se vytváří víry, ve kterých částice tekutiny proudí jinou rychlostí než v hlavním proudu a proto má tento vír i jinou teplotu než hlavní proud. Tento teplotní rozdíl umožňuje sdílení tepla mezi těmito dvěma rozdílnými proudy, což je typický nevratný proces způsobující nárůst entropie pracovní tekutiny, při kterém se část mechanické energie plynu transformuje na vnitřní teplnou energii. Takže, i když se postupně rychlost za clonou snižuje a tlak roste, nemůže celkový tlak dosáhnout původních hodnot.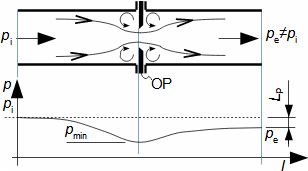

Škrcení tekutiny vloženou clonou – vznik trvalé tlakové ztráty
1: Škrcení tekutiny vloženou clonou – vznik trvalé tlakové ztráty
Klíčová slovaŠKRCENÍ PLYNŮ A PAR
6.4
OP-clona (orfice plate). l [m] délka úseku ovlivněného úseku; p [Pa] tlak; Lp [Pa] tlaková ztráta na sledovaném úseku. Index i označuje počáteční stav tekutiny, index e konečný stav tekutiny (na konci úseku/sledovaného děje).

Škrcení kapalin

Tlaková ztráta při škrcení kapalin je méně výrazná než při škrcení plynů, protože teplotní změny jsou u kapalin mnohem menší než u plynů.

h-s diagram

Při škrcení je celkový energetický obsah, respektive celková entalpie tekutiny, konstantní, viz h-s diagram celého procesu škrcení plynu na Obrázku 2. V tomto případě při škrcení plynu dochází nejen k poklesu tlaku ale ke změně teploty a měrného objemu, respektive hustoty, takže ve výsledku může být rychlost za clonou o něco vyšší než před clonou.

Energetická rovnováha škrcení plynu vloženou clonou
2: Energetická rovnováha škrcení plynu vloženou clonou
k-průběh stavových veličin plynu během škrcení. h [J·kg-1] entalpie; hs [J·kg-1] celková entalpie tekutiny (stagnation enthalpy); s [J·kg-1·K-1] entropie; t [°C] teplota; V [m·s-1] rychlost plynu; v [m3·kg-1] měrný objem. Index s označuje celkový stav tekutiny. Rovnost celkových entalpií je odvozena z Prvního zákona termodynamiky pro otevřený systém, odvození je provedeno v Příloze 4.

Kinetická energie

Při škrcení bývá změna kinetické energie plynu v důsledku zvětšení měrného objemu plynu pro většinu případů nevýznamná, přitom pojmem "většina případů" bývá myšleno proudění cca do 40 m·s-1 (lze tvrdit pro běžné stavy plynů – teplota nad 200 K) a lze psát hi≈he. Přičemž platí, že čím větší je tlak plynu, tím větší entalpie, a tím menší je podíl kinetické energie, viz Úloha 1.

Joulův-Thomsonův jev

Joulův-Thomsonův jev při škrcení reálných plynů je způsoben změnou tepelné kapacity plynu, která je funkcí tlaku a teploty. To znamená, že i při stejné entalpii musí být po škrcení teplota plynu jiná než před škrcením, viz Rovnice 3. Tento jev u ideálních plynů s konstantní hodnotou tepelných kapacit teorie škrcení neočekává a případné změny teploty jsou způsobeny pouze změnou kinetické energie.

Klíčová slovaŠKRCENÍ PLYNŮ A PAR
6.5
Škrcení reálného plynu vloženou clonou – změna teploty a tlaku zobrazené v h-s diagramu
3: Škrcení reálného plynu vloženou clonou – změna teploty a tlaku zobrazené v h-s diagramu
Pro přehlednost není vliv rychlosti plynu v těchto rovnicích uvažován. cp [J·K-1·kg-1] tepelná kapacita 1 kg plynu při stálém tlaku; t [°C] teplota.

Inverzní křivka

Například při škrcení vodní páry je zcela běžné, že se její teplota snižuje, což je dobře patrné v h-s diagramu H2O [Mareš et al., 1999]. Ovšem každý reálný plyn má oblasti, kde platí opak, tj. při škrcení se plyn ohřívá. Oblasti ohřívání od oblasti chlazení rozděluje v p-t diagramu tzv. inverzní křivka, přičemž na této křivce se plyn chová při škrcení jako ideální plyn, více v [Kalčík and Sýkora, 1973, s. 202].

Škrcení páry

Jestliže při škrcení dojde ke změně skupenství (například při škrcení mokré páry), lze očekávat také změnu teploty, viz Úloha 2.

Využití efektu škrcení v labyrintových ucpávkách

Princip labyrintové ucpávky

Konstrukce labyrintových ucpávek

Pomocí škrcení lze vytvořit velkou tlakovou ztrátu na krátkém úseku. Toho se využívá k bezdotykovému utěsnění hřídelů formou labyrintových ucpávek. Labyrintovou ucpávku si lze představit i jako sériové zapojení několika clon, tak aby v důsledku zvýšení tlakové ztráty došlo i ke zmenšení hmotnostního toku ucpávkou. Na Obrázku 4 je typická Konstrukce labyrintových ucpávek za účelem vysvětlení její funkce. Plyn proudí zleva doprava z prostoru o tlaku pi nejprve zúženým prostorem mezi vrcholem břitu a statorem, kde se část entalpie plynu transformuje na kinetickou energii. V prostoru mezi břity (v komůrce) dochází k víření plynu a velké tlakové ztrátě – ke zvýšení měrného objemu plynu a k zahlcení ucpávky. Tímto způsobem dochází k postupnému snižování tlaku až na tlak za posledním břitem pe. Přičemž množství uniklého pracovního plynu v ucpávce je přímo úměrné velikostí mezer δ.

Konstrukce labyrintových ucpávek
4: Konstrukce labyrintových ucpávek
Klíčová slovaŠKRCENÍ PLYNŮ A PAR
6.6
(a) konstrukce pravého labyrintu; (b) nepravý labyrint. 1-břit z tenkého plechu; 2-temovací drát; C-tzv. komůrka (chamber); S-stator (skříň stroje); R-rotor. dS, dR [m] průměr statoru, respektive rotoru; Δ [m] šířka břitu; δ [m] minimální mezera mezi břitem a statorem.

Ideální labyrintové ucpávky

Fannova křivka

V ideální labyrintové ucpávce by docházelo k úplnému maření kinetické energie izoentropické expanze na vrcholech břitů v jednotlivých komůrkách, respektive rychlost v komůrce by odpovídala jejímu průtočnému průřezu a tlaku, který je na vrcholu vstupního břitu, viz Obrázek 5. Tímto způsobem postupně klesá tlak a roste měrný objem plynu. Podle [Dejč, Michail, 1967, s. 330] lze dokázat, že křivky-b a -k na tomto obrázku jsou mimo jiné tzv. Fannovy křivky. Mezi tyto dvě křivky se zakreslí jednotlivé procesy, z čehož vyjde počet břitů. Počet břitů se zaokrouhluje nahoru na celé číslo, viz Úloha 3b, ve které je použito ještě další zjednodušení.

Průběh maření kinetické energie v ideální labyrintové ucpávce s 5 břity
5: Průběh maření kinetické energie v ideální labyrintové ucpávce s 5 břity
s-průběh změny statického stavu plynu během škrcení; K-křivka stavů plynu na vrcholech břitů; C-křivka stavů plynu v komůrkách (mezi břity). A [m2] průtočný průřez; m• [kg·s-1] hmotnostní tok. Indexy K označují stavy plynu na vrcholcích břitů (knife-edges), tj. v nejmenších průřezech a indexy C stavy plynu v komůrkách.

Reálné labyrintové ucpávky

Ve skutečnosti škrcení plynu v labyrintové ucpávce neprobíhá ideálně, ale v jednotlivých komůrkách probíhá škrcení podobně jako na Obrázku 2. To znamená, že lze očekávat rozdílný hmotnostní tok ideální a reálnou ucpávkou (odchylka záleží na typu konstrukce labyrintu a na jaké straně inverzní křivky pracovního plynu škrcení probíhá).

Klíčová slovaŠKRCENÍ PLYNŮ A PAR
6.7

Aurel Stodola

Carl Pfleiderer

Pro přesnější výpočet hmotnostního toku labyrintovými ucpávkami lze použít poloempirické vztahy, nejčastěji odvozené Aurelem Stodolou a Carlem Pfleidererem, viz Úloha 3(a). Vztahy odvozené Stodolou jsou uvedeny například v [Krbek et al., 1999, s. 110], [Škopek, 2007, s. 60]. Výpočet ucpávek podle Pfleiderera je uveden v [Pfleiderer and Petermann, 2005, s. 286], kde jsou uvedeny i další tvary bezdotykových ucpávek (hladká hřídel, šroubovicové těsnění atp.).

Konstrukce labyrintových ucpávek

Voštinová ucpávka

Břity labyrintových ucpávek mohou být vyráběny například z plechu, který je zatemován do rotoru nebo statoru, viz Obrázek 4. Břity také mohou být vysoustruženy přímo v hřídeli, mohou být na prstencích, které se připevňují na hřídel nebo dělené prstence připevňované na stator. Používají se také voštinové tvary komůrek apod.

Kartáčové ucpávky

Mimo klasické labyrintové ucpávky se používají ucpávky kartáčové. Nicméně princip funkce je týž, a jde o to vyvolat škrcení unikajícího plynu. Kartáčové ucpávky se také často kombinují s labyrintovými systémy.

Materiál ucpávek

Materiál břitu bývá vždy měkčí než materiál protistěny, o kterou během provozu může zavadit. Břit z měkčího materiálu se třením o stěnu z tvrdšího materiálu "obrousí" a nemusí tak dojít k nehodě, respektive k zadření hřídele nebo k poškození statoru – stačí vyměnit břit. Břity mohou mít i povlak z velmi měkkého materiálu. Mezera mezi břitem a stěnou se pohybuje (při provozu) v řádech desetin mm v důsledku kmitání hřídele a případně teplotní roztažnosti.

Vyšlehání ucpávek

Únik plynů přes labyrintové ucpávky se může měnit v důsledku poškození či opotřebení břitů (vyšlehání ucpávek) – funkce ucpávky se snižuje i pouhým zaoblením hrany břitu. Prodloužení intervalu opravy ucpávek lze dosáhnout přidáním dalších břitů.

Propojení labyrintových ucpávek

Mimo velmi jednoduchého provedení labyrintové ucpávky, kdy tekutiny z vnitřku stroje uniká do okolí nebo naopak, se používají labyrintové ucpávky s napojením na odsávání nebo naopak na zahlcování.

Klíčová slovaŠKRCENÍ PLYNŮ A PAR
6.8

Odsávání plynu z ucpávky

Napojení labyrintové ucpávky na odsávání unikající tekutiny se provádí za účelem aby pracovní tekutina nekontaminovala okolí stroje, nebo aby se ušetřila pro další použití. Odsávání znamená, že v odsávacím potrubí musí být nižší tlak, než je tlak okolního vzduchu, takže z druhé strany ucpávky je odsáván i vzduch, viz Obrázek 6. V případě parních turbín se potřebný podtlak vytvoří pomocí kondenzátoru ucpávkové páry. Pokud chceme odsávanou pracovní tekutinu ještě využít, musíme z ní vzduch odstranit, například u parních turbín se velmi čistá odsávána pára z ucpávek zbavuje vzduchu v kondenzátorech ucpávkové páry pomocí ejektorů (vývěv).

Základní zapojení ucpávkové páry parních turbín
6: Základní zapojení ucpávkové páry parních turbín
vlevo-zapojení na přetlakové části turbíny (tlak páry uvnitř stroje je vyšší než atmosférický); vpravo-zapojení na podtlakové části turbíny (tlak páry uvnitř stroje je nižší než atmosférický); pat [Pa] tlak okolí, v tomto případě atmosférický; 1-odsávání páry a přisátého vzduchu z ucpávek do ucpávkového kondenzátoru; 2-přívod zahlcovací páry.

Zahlcování ucpávky

Jestliže ve stroji je podtlak, pak k zabránění vniku vzduchu do stroje přes ucpávku se používá tzv. zahlcovací tekutina (obvykle je totožná s pracovní tekutinou), která je přiváděna do prostoru mezi počátkem a koncem ucpváky, viz Obrázek 6-vpravo. Tato zahlcovací tekutina má vyšší tlak než okolní vzduch, takže proudí směrem do stroje i směrem ze stroje – tím je zajištěno, že do stroje nepronikne vzduch. Aby nedošlo ke ztrátě velkého množství zahlcovací tekutiny do okolí přes ucpávku, tak je někde před koncem labyrintové části ucpávky odsávána společně s části vzduchu.

Regulační ventily

Hlavní funkcí regulačního ventilu je regulovat průtok za vzniku co nejmenší tlakové ztráty, respektive škrcení. Dalšími požadavky na regulační ventil jsou malá ovládací síla, velikost, těsnost, životnost a cena. Nicméně, ne vždy, lze vyhovět všem požadavků kladeným na regulační ventily a podle převažujícího požadavku rozlišujeme jednosedlové ventily, ventily s difuzorem, dvousedlové ventily a několik jejich variant provedení, viz Obrázek 7. Požadavkem na regulační ventil je predikce průtoku ventilem podle jeho otevření, což se obvykle stanovuje pomocí průtokového součinitele armatury.

Klíčová slovaŠKRCENÍ PLYNŮ A PAR
6.9
Základní typy regulačních ventilů
7: Základní typy regulačních ventilů
(a) jednosedlové ventily; (b) ventil s difuzorem; (c), (d) dvousedlové ventily – varianta (c) je vhodnější pro plynulou regulaci, varianta (d) pro systém otevřeno/zavřeno). 1-regulační orgán (v tomto případě kuželka); 2-difuzor.

Jednosedlové ventily

Jednosedlový ventil (Obrázku 7a) reguluje průtočný průřez jedním regulačním orgánem. Přivřením ventilu se sníží průtok a zvýší tlaková ztráta, respektive sníží se tlak za ventilem, což je způsobeno nehomogenním prouděním v oblasti nejužšího průřezu a vířením. Tlaková ztráta při částečně otevření ventilu je mnohem větší, než když je kuželka zcela vysunuta (proto se těmto ventilům také říká škrtící regulační ventily, zvláště prvnímu v řadě). Aby nevznikaly velké tlakové ztráty, tak nejvyšší rychlosti proudění ve ventilu (například při regulaci průtoku páry) mohou být jen cca do 50...70 m·s-1. To vede na velké průtočné průřezy ve ventilech a poměrně velké plochy kuželky jednosedlového ventilu, čímž se zvyšuje ovládací síla potřebná ke zdvihu kuželky. Jednosedlový regulační ventil se používá například k regulaci malých parních turbín.

Ventil s difuzorem

Přidáním difuzoru za hrdlo ventilu (Obrázek 7b, Obrázek 8) se dynamický tlak proudu plynu přeměňuje postupným zpomalením v difuzoru na statický tlak bez většího nárůstu entropie, takže se sníží tlaková ztráta ventilu. Rychlost proudění lze zvýšit na 100 až 150 m·s-1. Tyto vlastnosti umožňují při stejném průtoku zmenšit průřez ventilu (vzhledem k ventilu bez difuzoru), což zmenšuje potřebnou sílu na ovládání vřetene ventilu.

Klíčová slovaŠKRCENÍ PLYNŮ A PAR
6.10
Regulační ventil s difuzorem parní turbíny
8: Regulační ventil s difuzorem parní turbíny
Výrobce PBS. Obrázek: [Michele, 2010, s. 59].

Nenávrhový stav

Nevýhodou ventilu s difuzorem jsou efekty způsobené při nenávrhovém stavu, zvláště při výrazně nižších protitlacích než návrhových. Při poklesu protitlaku se může v hrdle ventilu nastavit kritické parametry proudění. V těchto případech se difuzor chová jako Lavalova tryska při nenávrhových stavech a v difuzoru, nebo za ním, může docházet ke vzniku rázových vln. To může způsobit vibrace ventilu a zařízení, které se za ventilem nachází případně i poškození ventilu a zvýšení ztrát. Při malých průtocích také vznikají velké víry iniciované zpětným prouděním pracovní látky za difuzorem zpět do difuzoru, tj. podobný efekt jako při odtržení mezní vrstvy od stěny difuzoru. Nepříjemným efektům v difuzoru při nízkých průtocích lze předejít zkrácením difuzoru. Na druhou stranu čím větší provozní rozsah ventilu je požadován, respektive čím kratší difuzor, tím větší budou ztráty spojené s krátkým difuzorem.

Dvousedlové ventily

Dvousedlové regulační ventily na Obrázku 7c-d mají oproti jednosedlovým výslednou sílu působící na vřeteno ventilu mnohem menší (síly působící na jednotlivé kuželky působí proti sobě). Nevýhodou jsou vyšší pořizovací náklady ventilu a problematická těsnost, i když obecně platí, že žádný typ regulačního ventilu většinou nelze dokonale uzavřít a potrubní trasa musí být opatřena i uzavíracími ventily.

Klíčová slovaŠKRCENÍ PLYNŮ A PAR
6.11

Průtok ventilem

Charakteristika ventilu

Především pro automatickou regulaci průtoku je důležitá znalost průtoku a tlakové ztráty ventilu v závislosti na velikosti jeho otevření. K tomu se používají rovnice ventilu, které jsou funkcí tlakové ztráty ventilu, hustoty tekutiny a tzv. průtokového součinitele armatury Kv, který lze odečíst z charakteristiky ventilu, což je závislot průtokového osučinitele armatury Kv na zdvihu vřetena armatury, viz Obrázek 9(c).

Průtokový součinitel armatury Kv, Kvs, Kv100

Průtokový součinitel armatury pro nestlačitelné tekutiny je objemový průtok ventilem, při referenční hustotě pracovní tekutiny a referenční tlakové ztrátě platný pro konkrétní polohu vřetena ventilu, viz Rovnice 9a. Z praktických důvodů většinou výrobci armatur do průtokového součinitele armatury Kv zahrnují i referenční konstanty, viz Rovnice 9b. Rozlišujeme okamžitý průtokový součinitel armatury pro daný zdvih regulačního orgánu Kv, průtokový součinitel pro případ plně otevřeného ventilu (H=Hmax) garantovaný výrobcem Kvs a skutečný průtokový součinitel naměřený při plném otevření ventilu Kv100 (je povolena odchylka od Kvs v rozmezí ±10 %). V ideálním případě platí rovnost Kv100=Kvs.

Určení průtoku regulačním ventilem z charakteristiky ventilu
9: Určení průtoku regulačním ventilem z charakteristiky ventilu
(a) fyzikálně přesná definice průtokového součinitele armatury Kv; (b) praktická definice průtokového součinitele armatury Kv; (c) příklad charakteristiky ventilu. Kv [m3·s-1] průtokový součinitel armatury; Kv100 [m3·s-1] průtokový součinitel armatury při plném otevření ventilu; Q [m3·s-1] objemový průtok ventilem; Δpref [Pa] tlakový rozdíl (ztráta) na ventilu při referenčním měření (obvykle 100 000 Pa); Δp [Pa] naměřený tlakový rozdíl na ventilu; ρ [kg·m-3] hustota tekutiny na vstupu do ventilu; ρref [kg·m-3] hustota tekutiny na vstupu do ventilu při referenčním měření (např. hustota vody obvykle při 15 °C); H [m] zdvih regulačního orgánu; H100 [m] maximální zdvih regulačního orgánu (ventil je plně otevřen). Odvození je uvedeno v Příloze 5.

Tlaková ztráta ventilu

Tlaková ztráta ventilu je měřena, pokud výrobce nestanoví jinak, mezi dvěma body nacházející se ve vzdálenosti 2·d před ventilem a 6·d za ventilem, kde d je průměr potrubí, aby víry vznikající při průtoku ventilem neovlivňovaly měření.

Klíčová slovaŠKRCENÍ PLYNŮ A PAR
6.12

Charakteristiky ventilu

Tvar charakteristiky ventilu je určen tvarem jeho regulačního orgánu (kuželky), takže lze dosáhnout i jiných než lineárních závislostí (např. parabolické), podle určitého požadavku na regulační ventil, který vychází z charakteristik zařízení v okolí ventilu více v [Doubrava et al., 2006].

Průtokový součinitel armatury

Průtokový součinitel armatury pro plyny nezávisí pouze na hustotě, ale je funkcí i entalpie plynu. Z těchto důvodů pro výpočet průtoku ventilem nestačí měřit jen tlakovou ztrátu, ale i teplotu. Vzorce průtokových součinitelů armatur pro průtok plynů jsou funkcí i teplot případně dalších veličin, viz vzorce v např. [Roček, 2002, s. 243], [Doubrava at al., 2006, s. 34].

Redukční ventily a redukční stanice

Redukce tlaku, respektive škrcení je žádoucí například při regulaci tlaky plynu před spotřebiči plynu napájenými z plynovodů pracujícíh o vyšším tlaku. Redukce tlaku je také důležitý děj k realizaci chladícího oběhu, linek na zkapalňování plynů, svařovacích agregátů a při redukci tlaku zemního plynu apod. Zařízení, ve kterém se provádí regulovaná redukce tlaku se nazývá redukční ventil. Redukční ventily mají odpovídající přesně vymezené umístění v rámci technologie v redukční stanici, což je soubor zařízení s redukčním ventilem opatřený potřebnými armaturami (uzavírací armatura, klapka atd.).

Redukční ventily

Na rozdíl od regulačních ventilů průtoku požadavek na redukční ventily tlaku je snížit tlak. Redukční ventil využívá škrcení tak, že snižuje nebo zvyšuje průtočný průřez zasouváním a vysouváním regulačního orgánu, což může být například kuželka, válcová děrovaná kuželka či labyrintový škrtící systém.

Membránový redukční ventil

Pohyb regulačního orgánu může být zajištěn servopohonem či pneumaticky na základě informací o tlaku v regulovaném prostoru nebo jiného požadavku z dozorny apod. Nejjednodušší redukční ventily mají ovšem přímou regulační vazbu. Například na Obrázek 10 je tzv. redukční ventil membránový, kde je průtok tekutiny regulován kuželkou. Kuželka je ovládána vřetenem, které reaguje na změnu výstupního tlaku. Výstupní tlak je odvozen od předpětí pružiny. Pokud je výstupní tlak nižší než nastavený, převáží síla pružiny nad sílou od tlaku a kuželka se pohne směrem nahoru, tím se zvětší průtočný průřez a průtok plynu. Pokud tlak pe je vyšší než nastavený, působí na pružinu větší síla, tím se stlačí a otvor pod kuželkou se zmenší.

Klíčová slovaŠKRCENÍ PLYNŮ A PAR
6.13
Redukční ventil membránový
10: Redukční ventil membránový
1-odběr tlaku (odběrové místo nebývá přímo za výstupním hrdlem, ale v místě, kde je nutné udržovat tlak pe např. napájecí nádrž atd.).

Membránový pojistný ventil

Redukční ventily pro redukci tlaku hořlavého plynu jsou vybaveny i bezpečnostními pojistkami, které uzavřou ventil v případě nežádoucích stavů plynu na výstupu nebo při požáru, takové sestavy se nazývají redukční pojistné ventily. Na Obrázku 11 je membránový redukční ventil s pojistkou-g, která se na signál odjistí a uzavře průchod plynu sedlem škrtícího ventilu. Po uzavření se musí ručně znova natáhnout a otevřít tak průchod plynu sedlem ventilu. Navíc je hlavní membrána-a zdvojena, aby se zamezilo úniku plynu v případě, že jedna praskne, jinak by hrozil únik plynu do oblasti pružiny a případně přes odvětrání-c i únik do okolí. Používají se ale i typy pojistek, které reagují na příliš nízký tlak plynu na výstupu i když je ventil zcela otevřen. Tento stav může nastat pokud tlak v plynovodu klesne pod bezpečnou hodnotu, například když doje k poškození plynovodu nebo spotřebiče za ventilem.

Membránový redukční ventil
11: Membránový redukční ventil
a-membrána; b-řídící pružina; c-vývod pro odvětrání; d-páka; e-táhlo ventilu; f-ventil; g-bezpečnostní pojistka – existují různé konstrukce podle toho jestli reagují na tlak či změnu teploty, například při požáru.
Klíčová slovaŠKRCENÍ PLYNŮ A PAR
6.14

Redukční stanice

Redukčním ventil lze v redukční stanici zapojit do režimu redukce tlaku či přepouštění, podle toho na jaké straně ventilu, z pohledu směru proudění, je nutné udržovat tlak, viz Obrázek 12.

Redukční ventil – možnosti zapojení
12: Redukční ventil – možnosti zapojení
(a) zapojení redukčního ventilu jako redukční stanice (udržování tlaku pe); (b) zapojení redukčního ventilu do funkce přepouštěcího ventilu (udržování tlaku pi). Platí pi>pe.

Vícestupňová redukční stanice

Redukční stanici lze rozdělit i do několika stupňů (na několik redukčních ventilů), v každém stupni se sníží tlak o určitou část. V případě sériového zapojení redukčních ventilů (do kaskády) je nutné počítat z obtížemi se synchronizací ovládání redukčních ventilů, proto se používá jen v případech odběrů nižšího tlaku mezi ventily, nebo pokud není dostupný jeden redukční ventil potřebných parametrům. To byl i například důvod použití několika vzduchových redukčních ventilů ze svařovacích agregátů zapojených za sebou ke snižování tlaku okysličovadla sovětské raketové stíhačky BI-1 – na podzim 1941 již nebyl čas vyvíjet speciální redukční ventil [Arlazorov, 1981, s. 127].

Redukčně-chladící stanice

Parní redukční stanice často obsahují i zařízení k chlazení páry. Takové zařízení se nazývá redukčně-chladící stanice, která je na Obrázku 13, podrobné schéma zapojení redukčně-chadící stanice je například v [Mikula et al., 1974]. Redukčně-chladící stanice obsahuje za redukčním ventilem ještě vstřikovací hlavice obvykle s ejektorem, ve kterém je hnacím médiem pára. Platí, že čím blíže je chladící voda mezi sytosti, tím rychleji se odpařuje a tím je úsek potrubí, na kterým může dojít ke styku kapek a potrubí kratší.

Redukčně-chladící stanice a h-s diagram popisující probíhající změny
13: Redukčně-chladící stanice a h-s diagram popisující probíhající změny
a-škrtící orgán (v tomto případě válcová děrovaná kuželka); b-táhlo ovládání škrtícího orgánu; c-jedna až tři clony, které zvyšují tlakovou ztrátu a snižují hlučnost na principu tlumiče hluku; d-přívod chladicí vody do vstřikovací hlavy; e-vstřikovací a rozstřikovací vodní tryska. h-s diagram: 0-počáteční stav páry; 1-pára po redukci tlaku; 2-pára na výstupu, tj. po redukci tlaku a chlazení; k-křivka přeměny chladící vody v přehřátou páru na stav 2.
Klíčová slovaŠKRCENÍ PLYNŮ A PAR
6.15

Turboexpandér

Škrcením a chlazením páry v redukčně-chladících stanicích se snižují parametry páry bez užitku. Proto se, pokud to jde, nahrazují redukčně chladící stanice malými parními turbínami. Takový způsob redukce tlaku se někdy označuje jako točivá redukce. Točivou redukci lze použít nejen u parních sítí, ale používají se i na plynových sítí, kde se nazývají turboexpandéry.

Škrcení v průřezových průtokoměrech

V případech nestlačitelného proudění (u plynů přibližně do 0,3 Mach) se k měření průtoku potrubím používají průřezová měřidla využívající transformace mezi tlakovou a kinetickou energii při proudění tekutiny zužujícím se průřezem. V nejužším místě měřidla bude podle Bernoulliho rovnice kinetická energie vyšší a tlaková energie nižší než před zúžením. Z rozdílu tlakové energie lze tedy vypočítat kinetickou energii proudění a následně rychlost, objemový a hmotnostní tok. Nevýhodou průřezových měřidel je jejich vyšší tlaková ztráta než stejně dlouhého hladkého potrubí, přičemž tlakové ztráty jsou u clon vyšší než u venturiho trubic, ale mají menší zastavěný prostor.

Venturiho trubice

Tryska

Clona

Konstanta průtokového měřidla

Jarkovský, 1958

Roček, 2002

Mezi průtoková měřidla měřidla patří například Venturiho trubice, clony, trysky, viz Obrázek 14, kde je uvedena i rovnice pro výpočet vstupní rychlosti tektuiny do  měřidla na základě změny tlaku. Kompletní výpočet všech tří hlavních typů proudových měřidel včetně konstrukčního  návrhu  a přibližného  výpočtu  konstanty měřidla-K je uveden v [Jarkovský, 1958]. Výpočet  proudění  clonou je uveden také v [Roček, 2002, s. 239].

Průřezová měřidla průtoku nestlačitelné tekutiny
14: Průřezová měřidla průtoku nestlačitelné tekutiny
(a) Venturiho trubice; (b) tryska; (c) clona. Δp na obrázcích neznačí vzniklou tlakovou ztrátu, ale rozdíl statických tlaků. Δp [Pa] rozdíl statických tlaků mezi měřenými místy; K [1] konstanta průtokového měřidla (je funkcí tvaru a rozměrů měřidla, druhu proudění a zúžení proudu – nutno změřit při kalibraci měřidla. Odvození rovnice rychlosti tekutiny v průřezovém měřidle pro ideální proudění kapaliny je uvedeno v Příloze 6.

Umístění průtokoměru

Podmínkou přesného měření je přímý úsek potrubí

Průtoková měřidla musí být zabudována do přímého úseku potrubí s přesně definovanými délkami uklidňujících úseků před a za měřidlem [Ďaďo et al., 2005].

Klíčová slovaŠKRCENÍ PLYNŮ A PAR
6.16

Clona

Průtokoměry se škrticí clonou jsou robustní a i při velkých průměrech potrubí relativně levné. Clonou lze měřit průtok většiny čistých tekutin. Clony jsou náchylné na opotřebení, které může být způsobeno abrazivními částicemi unášené tekutinou. To může ovlivnit tlakovou diferenci odpovídající určitému průtoku.

Kritická rychlost

Velice jednoduché je měření průtoku plynu, pro případ kritické rychlosti (dojde k ní v nejužším místě například u pojistných ventilů). V takovém případě stačí znát průtočný průřez, tlak a hustotu před nejužším průřezem a dopočítat průtok z rovnice pro kritický průtok tryskou.

Hydraulické vyvažování potrubí pomocí škrcení

Škrtící vložka

Škrtící ventil

Hydraulické vyvažování pomocí škrcení se používá zvláště u vzduchotechniky. Skutečný tlakový odpor vzduchovodů se ne vždy daří předem určit, proto se již při jeho stavbě počítá s dodatečným vložením škrtící vložky, viz Obrázek 15a, která například zajistí rovnoměrné proudění vzduchu v několika větvích rozvodu trvale vytvářenou tlakovou ztrátou (na větvi, která má menší odpor než okolní). Případně se na sání vzduchovodu mohou vložit některé z typů sacích škrtících ventilů s nastavitelnou tlakovou ztrátou Obrázek 15b.

Škrtící orgány v rozvodu vzduchu
15: Škrtící orgány v rozvodu vzduchu
(a) škrtící vložka; (b) nasávací ventil vzduchovodu s regulovatelným (na závitu) průtokem, respektive Lp.

Vyvažovací armatury

Na potrubních trasách kapalin mohou být vloženy škrtící ventily s nastavitelnou tlakovou ztrátou, tzv. vyvažovací armatury. Používají se především na rozvodech malých průtoků, na kterých je předimenzován (z různých důvodů) výtlačný tlak čerpadla.

Úlohy

Úloha 1:
Porovnejte mezi sebou měrnou entalpii a měrnou kinetickou energii přehřáté vodní páry proudící v potrubí. Teplota páry je 120 °C, tlak atmosférický, rychlost proudění 30 m·s-1. Účelem této úlohy je porovnat mezi sebou měrnou entalpii páry a její kinetickou energii při nízkých rychlostech. Řešení úlohy je uvedeno v Příloze 1.
Klíčová slovaŠKRCENÍ PLYNŮ A PAR
6.17
§1:   zadání:   pi; xi; pe §3:   odečet:   h
§2:   výpočet:   ek §4:   porovnání:   ek vs h
Popisek symbolů je uveden v Příloze 1.
Úloha 2:
Mokrá pára o tlaku 20 bar a suchosti 0,96 je seškrcena na sytou páru. Určete teploty na začátku a konci škrcení a přírůstek entropie při škrcení. Děj zakreslete do h-s a T-s diagramu. Řešení úlohy je uvedeno v Příloze 2.
Škrcení mokré páry
x [1] suchost páry; T [K] absolutní teplota. i'-bod syté kapaliny; i''-bod syté páry.
§1:   zadání:   V; t; p §3:   výpočet:   hi
§2:   odečet:   ti; h'i; h''i §4:   odečet:   te
Popisek symbolů je uveden v Příloze 2.
Úloha 3:
Vypočítejte hmotnostní tok labyrintovou ucpávkou parní turbíny, jestliže tlak před ucpávkou je 1 MPa, za ucpávkou 0,1 MPa, teplota páry před ucpávkou 260 °C, počet břitů 10 s plochým koncem, střední průměr těsnící kruhové spáry hřídele je 350 mm, velikost mezery mezi břitem a statorem je 0,2 mm, šířka břitu je 2 mm. Výpočet proveďte za (a) podle nějakého dostupného výpočtového modelu reálné ucpávky; (b) podle teorie ideální ucpávky. Řešení úlohy je uvedeno v Příloze 3.
§1:   zadání:   pi; pe; ti; Z; d; δ; Δ
  (a)     (b)  
§2:   výpočet:   ε; f §6:   odečet:   κ; vi; ε*s; χmax
§3:   porovnání:   ε vs. f §7:   výpočet:   AK; pi·vi
§4:   odečet:   μ; vi §8:   odhad:   m
§5:   výpočet:   AK; m §9:   výpočet:   p*K,n; vC,n-1; m*K,n; pK,n
    §10:   porovnání:   pK,10 vs. pe, jestliže pK,10 bude roven tlaku pe nebo roven p*K,10 odhad m na ř. 8 je správný, jinak zpět na ř. 8.
Popisek symbolů je uveden v Příloze 3.
Klíčová slovaŠKRCENÍ PLYNŮ A PAR
6.18

Odkazy

ŠKORPÍK, Jiří, 2024, Technická termomechanika, engineering-sciences.education, Brno, engineering-sciences.education/technicka-termomechanika.html.
ŠKORPÍK, Jiří, 2022, Úvod do lopatkových strojů, turbomachinery.education, Brno, ISSN 1804-8293. https://turbomachinery.education/uvod-do-lopatkovych-stroju.html.
ARLAZOROV, Michail, 1981, Konstruktéři, Naše vojsko, Praha.
ĎAĎO, Stanislav, BEJČEK, Ludvík, PLATIL, Antonín, 2005, Měření průtoku a výšky hladiny, BEN – technická literatura, Praha. ISBN 9788073001568.
DEJČ, Michail, 1967, Technická dynamika plynů, SNTL, Praha.
DOUBRAVA, Jiří, DYTRT, V., KLIMEŠ, M., MAREK, V., NOVOTNÝ, O., SUCHÁNEK, T., ŠALDA, M., 2006, Regulační armatury, LDM, spol. s r.o., Česká Třebová.
JARKOVSKÝ, Eduard, 1958, Základy praktického výpočtu clon, dýz a trubic Venturiho, Státní nakladatelství technické literatury, Praha.
KALČÍK, Josef, SÝKORA, Karel, 1973, Technická termomechanika, Academia, Praha.
KRBEK, Jaroslav, POLESNÝ, Bohumil, FIEDLER, Jan, 1999, Strojní zařízení tepelných centrál-Návrh a výpočet, PC-DIR Real, s.r.o., Brno, ISBN 80-214-1334-4.
MAREŠ, Radim, ŠIFNER, Oldřich, KADRNOŽKA, Jaroslav, 1999, Tabulky vlastností vody a páry, podle průmyslové formulace IAPWS-IF97, VUTIUM, Brno, ISBN 80-2141316-6.
MIKULA, Julius, KOČKA, Jaroslav, ŠKRAMLÍK, Emanuel, ŠTAUBER, Zdeněk, VESELÝ Adolf, OBR, Jan, 1974, Potrubí a armatury, Státní nakladatelství technické literatury, Praha.
PFLEIDERER, Carl, PETERMANN, Hartwig, 2005, Strömungsmaschinen, Springer Verlag Berlin, Heidelberg, New York, ISBN 3-540-22173-5.
ROČEK, Jaroslav, 2002, Průmyslové armatury, INFORMATORIUM, Praha, ISBN 80-7333-000-8.
ŠKOPEK, Jan, 2007, Parní turbína-tepelný a pevnostní výpočet, Západočeská uneverzita v Plzni, Plzeň, ISBN 978-;80-7043-256-3.

Doplňkový mediální obsah

©Jiří Škorpík, LICENCE