PROUDĚNÍ PLYNŮ A PAR TRYSKAMI

Copyright©Jiří Škorpík, 2006-2023
Všechna práva vyhrazena.

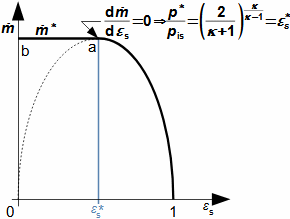
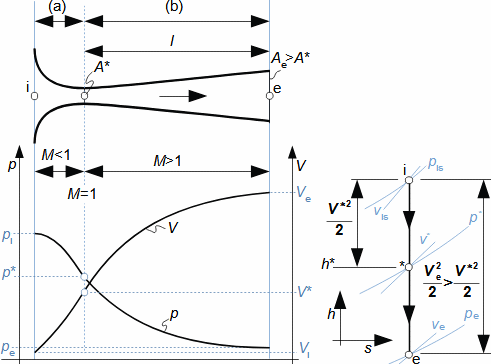
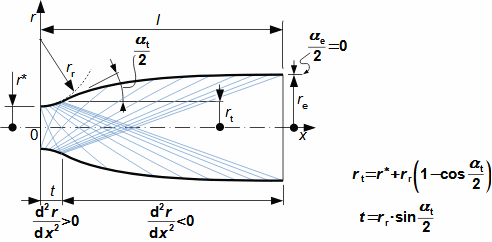
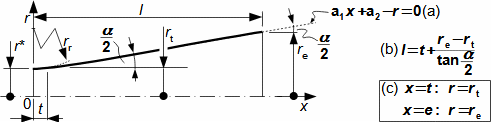
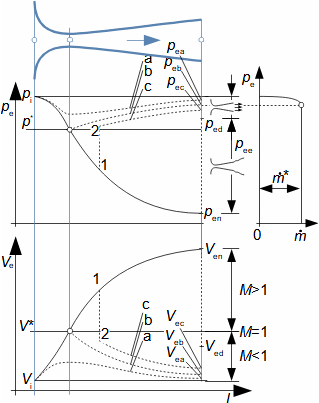
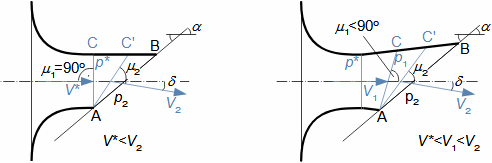
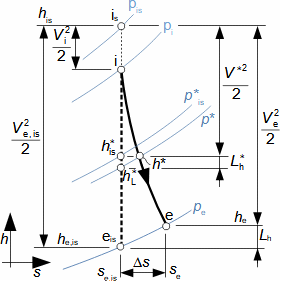
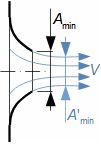
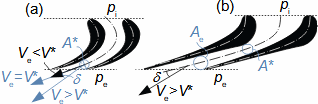
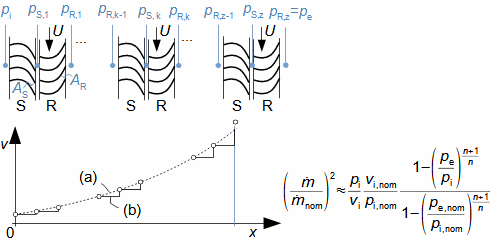
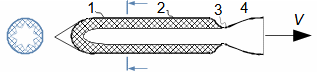
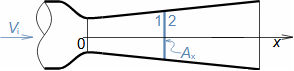
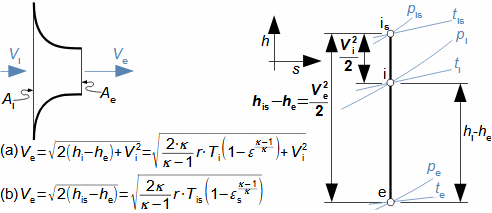
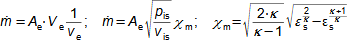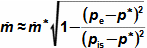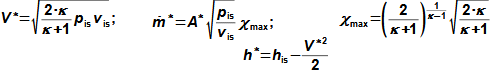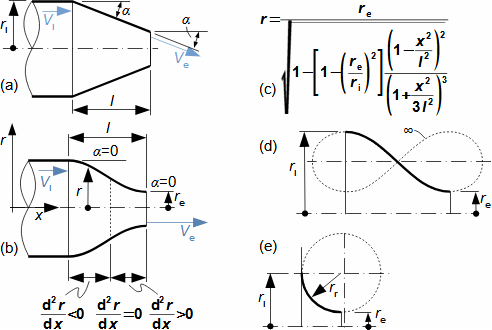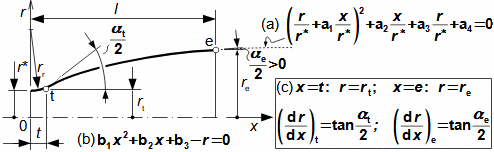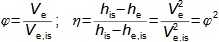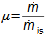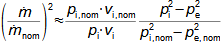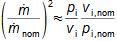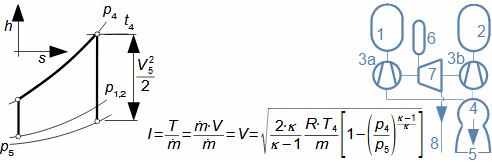1: Rovnice pro výtokovou rychlost trysky a definice tlakového poměru

(a) výpočet ze statického stavu plynu před tryskou; (b) výpočet z celkového stavu plynu před tryskou. e-stav v ústí trysky; i-stav na vstupu do trysky. A [m²] průtočný průřez trysky; h [J·kg^-1] entalpie; p [Pa] tlak; r [J·kg^-1·K^-1] individuální plynová konstanta plynu; s [J·kg^-1·K^-1] entropie; T [K] absolutní teplota plynu; t [°C] teplota; V [m·s^-1] rychlost; ε [1] tlakový poměr statických tlaků (p_e·p^-1_i); ε_s [1] tlakový poměr k celkovému vstupnímu tlaku (p_e·p^-1_is); κ [1] konstanta adiabaty (poměr tepelných kapacit). Index _s označuje celkový stav plynu (stagnation), index _i označuje stav na vstupu do trysky, index _e označuje stav na výstupu z trysky (těsně v ústí trysky). Odvození rovnice je v Příloze 6.

Na Obrázku 2 je znázorněn průběh výtokové rychlosti plynu V_e při změně protitlaku p_e, přičemž maximální rychlost plynu bude při výtoku do vakua p_e=0.

2: Výtoková rychlost plynu z trysky v závislosti na tlakovém poměru

p_at [Pa] atmosférický tlak. Parametry plynu: κ=1,4, r=287 J·kg^-1·K^-1, t_i=20 °C, p_i=p_at, V_i=0. Graf pro ideální plyn.

Hmotnostní tok tryskou

Hmotnostní tok plynu tryskou lze vypočítat z rovnice kontinuity. V případě ideálního plynu lze použít rovnice ideálního plynu pro rychlost a získat tak rovnici pro hmotnostní tok tryskou jako funkce tlakového poměru, viz Rovnice 3.

5: Maximální hmotnostní tok plynu tryskou

Odvození rovnice pro kritický tlakový poměr je uvedeno v Příloze 8.

Kritický tlakový poměr

Vodík

Vzduch

Vodní pára

Kritický tlakový poměr je funkcí druhu plynu, protože poměr tepelných kapacit κ se u jednotlivých plynů liší. Hodnoty kritických tlakových poměrů pro ideální plyn lze odečíst z Tabulky 4, protože právě při nich dosahují hodnoty průtokového faktoru maximálních hodnot. Kritické tlakové poměry reálných plynů se mírně liší, například pro vodík je 0,527, suchý vzduch 0,528, přehřátou vodní páru 0,546, sytou vodní páru 0,577. Nicméně lze počítat s tím, že kritický tlakový poměr se pohybuje kolem hodnoty 0,5.

Bendemannova elipsa

Křivka 1-a-0 z Obrázku 5 je tvarem velice blízkou elipse, proto se v inženýrské praxi, pro zrychlení a zjednodušení výpočtu trysky, úsek 1-a často nahrazuje části elipsy, která se nazývá Bendemannovou elipsou, viz Rovnice 6, jejíž platnost je omezena na rozsah p_e≥p^*.

6: Bendemannova elipsa

Odvození rovnice pro Bendemannovu elipsu je uvedeno v Příloze 9.

Kritická rychlost proudění

Průtokový kužel trysky

Rychlost zvuku

Při kritickém nebo nižším tlakovém poměru dosahuje rychlost proudu v nejužším místě trysky rychlosti zvuku, tento stav proudění se nazývá kritickým stavem. Dosazením kritického tlakového poměru (Rovnice 5) do Rovnice 1 a Rovnice 3 lze získat rovnice pro stanovení hodnot klíčových veličin pro nejužší místo trysky v případě dosažení nebo podkročení kritického tlakového poměru, viz Rovnice 7. Tyto veličiny se nazývají kritické (kritická rychlost, průtok, tlakový poměr...), přičemž v Tabulce 4 jsou nejvyšší uvedené hodnoty χ současně i χ_max pro dané κ. Grafické vyjádření závislosti průtoku na vstupním tlaku a protitlaku se nazývá průtokový kužel trysky, viz článek Technická matematika [Škorpík, 2023].

Lavalova tryska (konvergentně-divergentní tryska)

Jestliže tlak v okolí ústí konfuzorové trysky je nižší než kritický tlak, pak se v ústí trysky nastaví kritická (zvuková) rychlost a kritický tlak, takže plyn za tryskou dále expanduje a jeho rychlost se zvyšuje podle Rovnice 1 na nadzvukovou. Podle Hugoniotova teorému současně roste průtočný průřez takto vzniklého rychlého proudu plynu. Rozšiřující se proudový kanál vytváří na okrajích s okolním plynem šikmé rázové vlny, které se odráží dovnitř proudu a snižují účinnost expanze, viz Obrázek 9, na kterém je výtok vzduchu z konvergentní trysky do tlaku nižšího než kritického. Po vyrovnání tlaku s okolím expanze ustává a následuje postupná termodynamická rovnováha stavu plynu s okolním plynem. Pro zlepšení účinnosti expanze plynu za kritickým průřezem trysky, tedy pro případ p^*>p_e, je třeba pro expandující plyn vytvořit vhodné podmínky, tj. vytvořit za nejužším průřezem trysky rozšiřující se kanál – taková konstrukce se nazývá konvergentně-divergentní tryska nebo také Lavalova tryska. Používaných tvarů K-D trysek je více a závisí na účelu použití, technologické náročnosti výroby a maximální požadované délce trysky. Nicméně délka trysky také ovlivňuje její provozní rozsah, protože při jiném než návrhovém stavu tj. nenávrhovém stavu v K-D trysce nebo jejím okolí vznikají efekty spojené s vysokou rychlostí.

9: Výtok z trysky při kritickém tlakovém poměru

Obrázek z [Slavík, 1938, s. 5].

Charakteristika Lavalovy trysky

Divergentní část trysky umožňuje plynulou expanzi plynu do nadzvukových rychlostí v trysce bez větších ztrát, viz Obrázek 10. Přičemž v konvergentní části trysky je rychlost proudu podzvuková M<1, v divergentní části nadzvuková M>1 a v hrdle mezi nimi rychlost zvuku M=1. h-s diagram Lavalovy trysky trysky má stejný tvar jako h-s diagram zužující se trysky na Obrázku 1, stejně tak platí i rovnice pro rychlost, akorát plyn při expanzi překonává kritické parametry.

Metoda charakteristik

Aerodynamický tunel

Tvar K-D trysek vymodelovaný metodou charakteristik (Obrázek 12) je ideálním tvarem. Trysky navržené touto metodou mají totiž rovnoměrné rychlostní profil na výstupu. Metoda charakteristik je založena na postupné konstrukci expanzních vln, tyto vlny jsou na Obrázku 12 zakresleny modře. Okrajovou podmínkou této metody je zadaný počáteční poloměr r_r při α_e=0° (podmínka výstupní rychlosti v osovém směru) a průtočný průřez na výstupu A_e [Dejč, 1967, s. 341], [Sutton and Biblarlz, 2010, s. 79]. Nevýhodou je, že délka takové trysky je mnohem větší než trysky kuželové, takže v důsledku vnitřního tření může být její účinnost nižší než u kuželových trysek, proto se tento tvar trysek používá prakticky jen v nadzvukových aerodynamických tunelech, kde je rovnoměrné rychlostní pole na výtoku velmi důležité.

12: Ideální tvar divergentní trysky

α [°] úhel rozšíření trysky; t [m] vstupní délka rozšiřující se části trysky (obvykle kruhový obrys o poloměru r_r≈0,382·r* [Sutton and Biblarlz, 2010, s. 80]). Odvození rovnic pro r_t a t jsou uvedeny v Příloze 10.

Rovnice kuželové trysky

Kuželový tvar K-D trysky je jejím nejjednodušším tvarem, viz Obrázek 13. Tyto trysky jsou charakteristické snadným výpočtem i výrobou, protože mají stálý úhel rozšíření. Používají se i jako statorové kanály jednostupňových turbín, v případech kdy jsou jiné ztráty tak vysoké, že není hospodárná výroba složitějšího tvaru. Tento tvar se používá i u malých raketových motorů, malých trysek, na injektorech a ejektorech a podobně. Nevýhodou tohoto tvaru trysky je, že nelze na výstupu dosahovat rovnoměrného rychlostní pole a odklon rychlosti od osy kanálu způsobuje ztrátu na hybnosti v osovém směru (při úhlu α=20° asi 1 % [Sutton and Biblarlz, 2010, s. 78]). Výpočet vychází ze zadaného úhlu rozšíření α, který bývá 8 až 30° a z vypočítaného průtočného průřezu na výstupu A_e. Tyto dva parametry stačí k výpočtu délky divergentní části trysky.

Nenávrhový stav trysky

U správně navržené K-D trysky dosáhne v ústí trysky tlak proudící tekutiny právě tlaku p_e,n (návrhový tlak). Nenávrhovým stavem trysky je tedy myšlen stav, kdy se mění vstupní parametry plynu nebo výstupní parametry plynu nebo oba parametry najednou. Tyto parametry se mohou měnit z různých příčin (regulace průtoku tryskou apod). Celkem mohou nastat dva základní případy nenávrhových stavů K-D trysky a to přeexpandovaný stav a podexpandovaný stav.

Přeexpandovaná tryska

Jestliže tlak na výstupu z trysky p_e je vyšší než návrhový tlak p_en, pak hovoříme o tom, že tryska je přeexpandovaná (tryska byla navržena na "delší" expanzi, než je skutečnost). Přeexpandovaná tryska může mít jeden z pěti možných provozních stavů popsaných na Obrázku 15 případy a až e, respektive protitlaky p_e,a až p_e,e. Přičemž případy c až e jsou charakteristické tím, že vznikají kolmé rázové vlny podle protitlaku, buď v trysce, na jejím okraji (případ e) a nebo až za tryskou. Vznik rázových vln při těchto nenávrhových protitlacích lze predikovat z Hugoniotova teorému. Rázová vlna v trysce nebývá stabilní a může proto vyvolávat vibrace trysky a přilehlých částí dalších strojů, navíc podstatně zvyšuje hlučnost. Při hledání polohy kolmé rázové vlny v trysce, lze vycházet z Rankine-Hugoniotových rovnic, viz Úloha 4.

15: K-D tryska – charakter proudění při změně protitlaku

Index ₁ označuje stav před rázovou vlnou; ₂ za rázovou vlnou.

Proudění tryskou se ztrátami

Pomineme-li nenávrhové stavy v trysce, pak ztráty, které v tryskách vznikají jsou způsobené zejména vnitřním třením plynu. Mimo termodynamické ztráty dochází ještě ke snížení průtoku kvůli kontrakcí proudu za nejužším průřezem trysky.

Vnitřní tření v trysce

h-s diagram trysky

Vnitřní tření plynu a tření o stěny trysky způsobují disipaci energie ve formě třecího tepla, což zvyšuje entropii plynu a snižuje tak výslednou kinetickou energii plynu, viz Obrázek 17. Navíc se v proudu mohou vyvinout víry, ve kterých dochází k nežádoucím transformacím energie na stejném principu jako při škrcení, což také vede na zvyšování entropie.

17: Proudění v trysce se ztrátami

L_h [J·kg^-1] měrná ztráta v trysce. Index _is označuje stav plynu pro případ izoentropické expanze.

Kritická rychlost

Při proudění ze ztrátami se v trysce vytváří rychlostní profil, takže při tlaku p^*_is může nastat v jádru proudu rychlost zvuku přičemž na okrajích (v blízkosti stěn) je rychlost podzvuková a střední rychlost v hrdle trysky je menší, než je rychlost zvuku, respektive střední kinetická energie plynu je nižší, než odpovídá energii při rychlosti zvuku. Až při tlaku p^*, který je nižší než je p^*_is, je střední kinetická energie plynu taková, že odpovídá rychlosti zvuku v celém průtočném průřezu plynu. Navíc, jestliže v kritickém bodě h^* má plyn jiné termokinetické vlastnosti než v bodě h^*_is, pak kinetická energie rychlosti zvuku bude jiná než při izoentropické expanzi. To znamená, že se změní i entalpie h*≠h*_is, ale tyto rozdíly mezi uvedenými body jsou velmi malé.

Tryska jako lopatkový kanál

Lopatkový kanál

Deviační úhel

Lopatkový kanál může mít tvar čistě konvergentní trysky i konvergentně-divergentní trysky. Takový lopatkový kanál se chová jako šikmo seříznutá tryska, viz Obrázek 21. Lopatkové kanály ve tvaru K-D trysky jsou používány v případech, kdy na jeho výstupu musí být nadzvuková rychlost pracovního plynu – například se používají u malých jednostupňových turbín a u posledních stupňů parních kondenzačních turbín.

21: Situace na výstupu z lopatkové mříže při nadzvukovém proudění

(a) konfuzorový lopatkový kanál; (b) lopatkový kanál pro nadzvukové rychlosti. δ [°] odklon nadzvukového proudu od osy kanálu, respektive zvětší deviačního úhlu lopatkové mříže.

Hmotnostní tok skupinou trysek, stupňů turbín a Stodolovo pravidlo

Hmotnostní tok turbínou

Teorie trysek se využívá i pro stanovení průtoku skupinou stupňů turbín za změněných podmínek před či za touto skupinou stupňů. Existuje hned několik výpočtových postupů, které ovšem byly vytlačeny numerickými výpočty. Proto si zde popíšeme pouze postup nejjednodušší, který má smysl používat při přibližných výpočtech, viz aplikace v článku Parní turbína v technologickém celku [Škorpík, 2011].

Sériové řazení trysek

Stupeň turbíny

Lopatkové kanály jednoho stupně turbíny jsou tvořeny statorovou a rotorovou řadou lopatek, přičemž ta rotorová je umístěna na hřídeli, která se otáčí, viz Obrázek 22 a článek Úvod do lopatkových strojů [Škorpík, 2022]. Lopatkové kanály v těchto řadách lze přirovnat ke dvou tryskám pracující v sérii, což znamená, že se jedná o trysky se stejným průtokem. Stejný předpoklad lze aplikovat i na skupinu s více stupni, respektive na více trysek řazených za sebou.

Exponent polytropy

Měrný objem

Uspokojivého výsledku přibližného výpočtu změny průtoku větší skupinou stupňů lze dosáhnout při zavedení dvou zjednodušujících předpokladů. Prvním je předpoklad adiabatické expanze a její konstantní hodnota exponentu polytropy i při změně průtoku. Druhým předpokladem je zjednodušení postupné změny měrného objemu plynu ve stupni na změnu skokovou, při které se měrný objem mění skokově vždy na výstupu z lopatkového kanálu, viz Obrázek 22.

Tryska raketového motoru

Specifický impuls

Vodík

Kyslík

Tah raketového motoru je roven hybnosti proudu výstupních spalin. Hlavní částí motoru je spalovací komora a na ni navazující K-D tryska. Ve spalovací komoře hoří okysličovadlo a palivo, tak vznikají spaliny, které expandují v trysce. Požadavkem na raketové palivo je, aby rychlost spalin byla co největší, protože to je způsob jak dosáhnout co nejvyššího poměru tahu ku spotřebě paliva (tento poměr se nazývá specifický impuls, viz Obrázek 25). Z úpravy rovnice pro rychlost spalin na výstupu z trysky je zřejmé, že jako palivo pro raketové motory jsou vhodné látky s vysokou teplotou hoření a malou molovou hmotností (například vodík, který má teplotu hoření s kyslíkem t_H2O=3244 °C při molové hmotnosti m_H2O=18 kg·mol^-1).

25: Raketový motor na kapalné palivo a výpočet rychlosti výtoku spalin

Raketový motor na kapalné palivo a výpočet rychlosti výtoku spalin: 1-okysličovadlo; 2-palivo; 3a-turbočerpadlo okysličovadla; 3b-turbočerpadlo paliva; 4-spalovací komora; 5-výstup spalin z K-D trysky; 6-zdroj horkých plynů pro turbínu (u jiných motorů může být palivem pro turbínu palivo raketového motoru); 7-turbína; 8-výfuk turbíny. T [N] tah; R [J·mol^-1·K^-1] univerzální plynová konstanta; m [kg·mol^-1] molová hmotnost spalin.

Motor SSME

Výkon raketového motoru je pak dán tlakem ve spalovací komoře a její velikostí. Například požadovaný tlak ve spalovací komoře motoru SSME raketoplánu Space shuttle byl 20,3 MPa a výkon turbíny turbočerpadla vodíku dosahoval 56 MW, při tahu 2278 kN [Růžička and Popelínský, 1986, s. 25], [Sutton and Biblarlz, 2010].

Raketové motory na tuhé látky

Existují i raketové motory na tuhá paliva (TPL), ve kterých probíhá postupné odhořívání palivové směsi za vzniku velmi horkých spalin (Obrázek 26). Vektor tahu se u motorů s TPL často reguluje pomocí šikmé rázové vlny řízeně vznikající vstřikováním kapaliny na vnitřní stranu trysky. Hvězdičkový průřez náplně paliva umožňuje postupné odhořívání palivové směsi a stabilní hoření. Tento hvězdicový tvar byl soustavně vyvíjen za druhé světové války v Anglii a vyvrcholil konstrukci balistické rakety na TPL typu Sergant [Holt, 2017, s. 94-110].

x [m] souřadnice osy x.

Odkazy