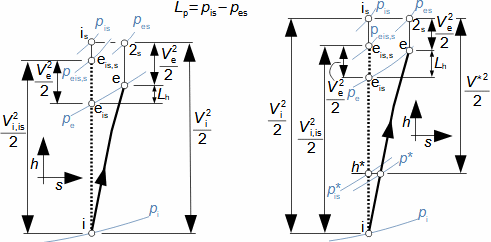
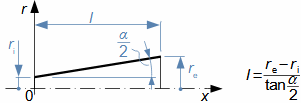
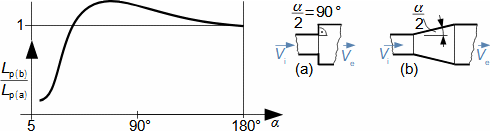
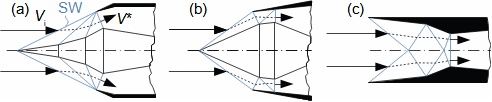
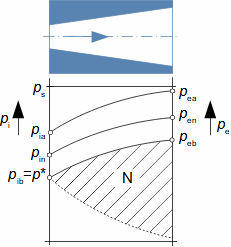
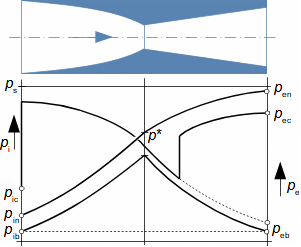
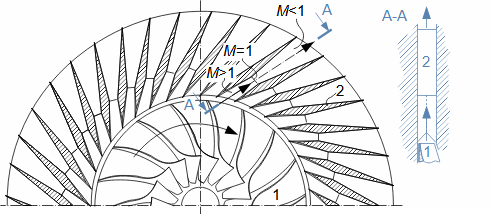
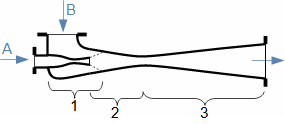
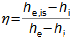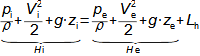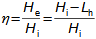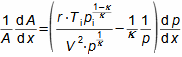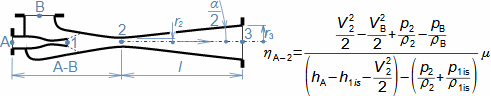Flow of gases and steam through diffusers

Škorpík, Jiří

KeywordsFLOW OF GASES AND STEAM THROUGH DIFFUSERS

5.3

What are diffusers and applications of diffuser theory

Subsonic and Supersonic diffuser

A diffuser is a channel with a continuously changing flow cross-section. Fluid flow in the diffuser is a process that primarily involves an increase in pressure and a decrease in kinetic energy. According to Hugoniot's theorem^3., a different shape of diffuser suits supersonic flow than for subsonic flow, because in a supersonic diffuser the flow must first slow down to the speed of sound^3. in the tapering part of the diffuser, see Figure 1.

1: Two basic types of diffusers

left-subsonic diffuser, short diffuser; right-supersonic diffuser. A [m²] diffuser flow area; V [m·s^-1] gas velocity; M [Mach] Mach number^3.; A* [m²] critical cross-section of supersonic diffuser in which gas reaches speed of sound (critical state). The index _i denotes the state at the inlet of the diffuser, the index _e denotes the state at the outlet of the diffuser.

Diffuser channel

Diffuser theory has wide application in various types of current machines with diffuser channel shapes. The sophisticated diffuser theory can be used to describe even, at first sight, very complex flows, for which a large amount of measured data is available for different diffuser shapes.

In this article are often used the same terms as in the article Flow of gases and steam through nozzles^4. - this is due to the fact that in the ideal case the process occurring in diffusers is opposite to the process occurring in the nozzle and therefore the equations for calculating the state of the gas are the same or are similar.

Energy balance of diffusers

The energy balance of diffusers is based on the first law of thermodynamics and its basic result is the diffuser efficiency. Often the term hydraulic diffuser efficiency is also used if the density changes inside the diffuser are insignificant.

Diffuser efficiency

Diffuser losses

Isoentropic compression

Pressure loss

h-s diagram of diffuser

The compression in the diffuser is affected by energy dissipation or losses. An h-s diagram can be used to identify the actual gas states as it flows through the diffuser and the losses, where the comparative (ideal) process is an isentropic compression with the same pressure and velocity at the outlet as the actual compression, see Figure 2. The pressure loss^1. L_p is then defined as the loss between the total outlet and inlet pressure of the diffuser. To overcome the loss L_p and achieve the same pressure as in lossless compression, the kinetic energy at the diffuser inlet must be increased by just the value of L_h.

KeywordsFLOW OF GASES AND STEAM THROUGH DIFFUSERS

5.4

Change of gas state in supersonic diffuser

2: Change of gas state in diffuser

left-diagram of h-s subsonic diffuser; right-diagram of h-s supersonic diffuser. h [J·kg^-1] gas enthalpy; h* [J·kg^-1] critical enthalpy; p [Pa] gas pressure; s [J·kg^-1·K^-1] entropy; t [°C] gas temperature; V* [m·s^-1] critical velocity^4.; L_h [J·kg^-1] diffuser loss; L_p [Pa] pressure loss. The index _s indicates the total gas state, the index _is the isentropic compression.

Mass flow through diffuser

The mass flow of gas through the diffuser depends on the size of the smallest diffuser flow area, which is the inlet flow area A_i for subsonic and the critical diffuser flow area A* for supersonic. The mass flow is then calculated from the continuity equation for the gas parameters at this flow area.

Critical flow speed

The critical velocity V*in actual compression is the same as in isoentropic compression, because the speed of sound in an ideal gas is a function of temperature only and the isotherms correspond to the isoenthalps in the h-s diagram. This means that the transition from supersonic to subsonic flow in real compression occurs at a lower pressure than in isentropic compression p*<p*_is. This is due to the lower gas velocity at the diffuser walls than at the core of the flow, therefore the mean gas velocity may already be sonic at pressure p*while it is still supersonic at the core of the flow. The above facts mean that the gas reaches the speed of sound - meaning the mean flow velocity - already before the narrowest point of the diffuser.

Diffuser efficiency

Diffuser efficiency can be defined in different ways. Most often it is the ratio between the difference in enthalpies at isentropic and actual compression, as these states are the easiest to detect, see Equation 3.

3: Diffuser efficiency

η [1] diffuser efficiency defined to static gas states (efficiency determined to total enthalpy states will have a higher value, as can be seen from the h-s diagram).

KeywordsFLOW OF GASES AND STEAM THROUGH DIFFUSERS

5.5

Similar diffusers under similar operating conditions will also have similar efficiencies. This similarity can be used in the design of a new diffuser to predict its parameters based on an estimate of its efficiency. The accuracy of such a design depends on the degree of similarity of the diffusers being compared.

Hydraulic diffuser efficiency

In the case of liquids or insignificant changes in gas density, the energy balance of the diffuser is based on Bernoulli's equation. In the diffuser, the liquid does not do any external work, so the total energy of the liquid in front of the diffuser must be equal to the total energy of the liquid at the outlet of the diffuser plus losses, see Formula 4.

Energy balance of the diffuser during fluid flow

4: Energy balance of diffuser during fluid flow

g [m·s^-2] gravitational acceleration; H_{i, e} [J·kg^-1] head of fluid at inlet or outlet; z [m] height of diffuser axis from reference plane; ρ [kg·m^-3] density.

In these cases, the diffuser efficiency, referred to as the hydraulic efficiency, can be defined as the ratio between the total energy of the fluid at the outlet and the inlet of the diffuser (Formula 5).

5: Hydraulic efficiency of diffuser

Diffuser shapes

In practice, only two diffuser shapes are used. The simplest shape is the conical diffuser with a constant diffuser angle. The other diffusers, also known as cornut diffusers, have a variable angle diffuser depending on the pressure gradient requirement of the diffuser.

Pressure gradient in diffuser

The properties of diffusers depend on the pressure gradient distribution in the diffuser, which can be determined for the case of lossless flow and ideal gas using Equation 6. In the case of actual processes, the pressure gradient can be calculated using thermodynamic data of real gases, see Problem 2.

KeywordsFLOW OF GASES AND STEAM THROUGH DIFFUSERS

5.6

6: Pressure gradient in diffuser

κ [1] ratio of heat capacities. The derivation of this equation is given in Appendix 4. The equation is derived under the simplifying assumption that the flow velocity has only an axial direction throughout the cross section and for an ideal gas.

Cone diffusers

Diffuser angle

The conical shape of the diffuser (Figure 7) is easy to produce, even in the case of non-circular variants. According to [Dejč, 1967, p. 391], the diffuser angle α ranges from 6 to 15°, while most diffusers are produced with the diffuser engle in the middle range of 10 to 12°.

7: Cone diffuser

r [m] radius; α [°] diffuser angle; l [m] diffuser length; x [m] distance on axis.

Flow separation

The very rapid pressure drop at the inlet of the cone diffusers causes that there is already a very small pressure gradient (see Problem 1) or very low flow energy at the end of the diffuser. This causes an increased probability of flow separation from the diffuser walls. This is a disadvantage of cone diffusers.

Cornut diffusers

Pressure gradient

Cone diffusers

Diffusers with the variable diffuser angle α are called cornut diffusers and are designed for the required pressure gradient. Most often, cornut diffusers are designed for a constant pressure gradient (Figure 8a) or a linear pressure gradient (Figure 8b). Cornut diffusers have a sharp widening at the outlet (see Problem 2), so they can be expected to be more sensitive to boundary layer separation from the wall than cone diffusers. Measurements show that this is the case for long diffusers, but the opposite is true for short diffusers (cone diffusers with α>18°) [Dejč, 1967, p. 392].

KeywordsFLOW OF GASES AND STEAM THROUGH DIFFUSERS

5.7

Diffuser with linear pressure gradient change

8: Cornut diffusers

(a) diffuser with constant pressure gradient, see its calculation in Problem 2; (b) diffuser with linear decrease in pressure gradient.

Constant pressure gradient

Velocity profile

Diffusers with the constant pressure gradient also have a more uniform velocity profile than cone diffusers and are therefore also used upstream of coolers or heat exchangers with the requirement for uniform distribution of mass flux over the flow area of the exchanger [Goroščenko, 1952, p. 67], [Frass, 1989, p. 155].

Linear pressure gradient

Flow separation

In the diffuser designed to linearly decrease the pressure gradient (Figure 8b), the pressure gradient decreases gradually as the boundary layer energy decreases (approximately linearly), and is therefore the shape with the lowest probability of boundary flow separation [Dejč, 1967, s. 388].

Continuous shape changes of diffusers with variable diffuser angles are difficult to manufacture and are therefore replaced by a combination of two or more conical diffusers with different diffuser angles, see Figure 9, [Dejč, 1967, s. 393].

9: Practical solutions for variable widening diffusers

Flow separation

Internal friction

Velocity profile

In diffusers, losses are caused by internal friction, possibly by shock waves, and by the loss due to the boundary layer separation from the diffuser walls. The process of boundary layer separation from the wall is shown in Figure 10. Boundary layer separation occurs as a result of the total pressure in the boundary layer dropping below the static pressure behind the diffuser. At this point, the working fluid backflows along the diffuser wall and the boundary layer is separated from the wall. The total pressure drops in the boundary layer due to the loss of kinetic energy of the flow. The loss due to boundary layer separation results in an increase in diffuser pressure drop.

KeywordsFLOW OF GASES AND STEAM THROUGH DIFFUSERS

5.8

10: Mechanism of boundary layer separation from diffuser wall and subsequent vortex formation

VP-velocity profile.

Turbulent flow

Laminar flow

Throat

The loss in boundary layer separation is greater the further away from the diffuser end the separation occurs. The position of the separation can be influenced, for example, by increasing the momentum of the flow at the diffuser walls, therefore turbulent flow is less sensitive to boundary layer separation than laminar flow - in turbulent flow there is a sharing of momentum between the edge and the core of the flow. If it is required to achieve turbulent flow, then it is necessary to ensure that the flow is already fully developed at the diffuser inlet. This is most often achieved by adding a throat before the diffuser in which the boundary layer development takes place until turbulence occurs, see Figure 11.

11: Development of velocity profile in diffuser throat

LF-laminar flow region; TRF-transition flow region; TP-fully developed turbulent flow. x_e [m] minimum diffuser throat length for full boundary layer development.

Turbulators

Draft tube

Tangetial velocity

Sucking

The turbulence of the flow can also be increased by various embeddings in the diffuser, the so-called turbulators, see [Dejč, 1967, p. 395], [Japikse and Baines, 1995]. Some embeddings give the flow a tangential velocity component and the centrifugal force will cause a higher pressure at the diffuser walls. Typical examples are water turbine suction tubes, in which a small tangential component of the flow at the turbine outlet is used to stabilize the boundary layer. The flow at the outlet of the diffuser can also be stabilised by sucking gas through openings in the diffuser walls, etc.

Skvělou ukázkou stabilizace proudění u stěn difuzoru je zadní křídlo formulí/rear wing. To funguje jako difuzor a rozdělením jeho profilu do více umožňuje přisávat proudění pod křídlo, a tím stabilizovat mezní vrstvu,která je odolnější vůči odtržení/stall. https://t.co/qlDcJsIIn0 pic.twitter.com/ULrvy1Zeej
— Jiří Škorpík (@jiri_skorpik) February 7, 2023

KeywordsFLOW OF GASES AND STEAM THROUGH DIFFUSERS

5.9

Pressure loss

The flow separation will also affect the magnitude of the pressure loss L_p of the diffuser (see Equation 2 for definition). Pressure loss is also a function of diffuser length and diffuser angle. Figure 12 shows the dependence of the pressure loss L_p of the diffuser with the change of the diffuser angle α. This pressure loss is compared with the pressure loss at the flow through two connected channels without a diffuser (α=90°). In this way, it is possible to evaluate up to which diffuser angle it makes sense to use diffusers and when not to use it.

12: Effect of cone diffuser angle on pressure loss

A scale diagram is given in [Dejč, 1967, p. 382].

Throttling

According to Figure 12, the pressure drop of the cone diffuser from a certain angle can be greater than that of the flow through two connected channels without a diffuser. This is due to the fact that the internal friction loss decreases with the diffuser angle α, but the vorticity loss at boundary layer separation increases with the angle α. Thus, in a flow through two connected channels without a diffuser, only the vortices at separation are generated [Maštovský, 1964, p. 88], which cause an increase in entropy by the same mechanism as in the throttling of the flow through the orifice.

Short diffusers

If it is necessary to shorten the diffuser, it is more cost effective to use the combination shown in Figure 13 than to increase the diffuser angle. This solution can be likened to a smooth cornut diffuser on Figure 8a.

13: Practical solutions for space-constrained diffusers

KeywordsFLOW OF GASES AND STEAM THROUGH DIFFUSERS

5.10

Supersonic diffusers

Method of characteristics

Oblique shock waves

The design of the supersonic diffuser is problematic. Ideally, the compression in the diffuser should be through compression waves^3., which are the opposite of expansion waves. The compression waves should occur in the convergent part of the diffuser, which corresponds to the inverted ideal CD nozzle designed by the method of characeteristics^4.. However, such supersonic diffusers are not produced because in real flow, oblique shock waves^3. are already generated at the inlet edges of the diffuser and others inside the convergent part [Dejč, 1967, p. 405].

Stepped diffusers

Supersonic flight

In realistic conditions, the best flow stability is achieved by supersonic diffusers that have stepped flow deceleration (Figure 14). These are shaped to produce successive oblique shock waves at certain points with progressively greater slope, so that the last wave at the narrowest point of the diffuser is normal^3.. Supersonic stepped diffusers are easy to design because the behaviour of oblique shock waves is well studied and described. Thus, in these cases, the losses that shock waves can cause are always taken into account. The diffusers in Figure 14 are jet engine diffusers and ensure that subsonic flow will enter the engine even during supersonic flight.

14: Supersonic diffusers with stepped flow deceleration

(a) stepped supersonic diffuser; (b), (c) stepped supersonic diffuser with following shock waves-as if reflected from diffuser wall- which inherently directs velocity vector in axial direction and reduces losses [Dejč, 1967, p. 409]. SW-shock waves.

Non-design diffuser conditions

Each diffuser is designed for a specific gas state in front of and behind the diffuser. If this state changes, the flow in the diffuser will change. Such a state is called a non-design state. In non-design conditions, the diffuser efficiency decreases (especially at lower flow rates, the loss due to boundary layer separation from the walls increases) and the diffuser may even turn into a CD nozzle^4..

KeywordsFLOW OF GASES AND STEAM THROUGH DIFFUSERS

5.11

Subsonic diffuser

Valve with diffuser

Figure 15 shows the two non-design conditions of the subsonic diffuser, denoted by a, b (index n indicates the design condition). These non-design conditions are induced by a change in the inlet velocity V_i for the same inlet stagnation pressure, where V_ia<V_in<V_ib=a. The velocity V_ib is sonic respectively critical. For each case, the backpressure also changes, if it were still the same (p_e=p_en), there would be no flow equilibrium. If we want to maintain backpressure, then we need to use inlet flow control-such a typical application is a diffuser valve. At less than the critical pressure p* a shock wave is generated behind the narrowest cross-section and, in addition, when the backpressure drops below p_ec, the diffuser becomes a CD nozzle, see Hugoniot's theorem.

15: Effect of inlet velocity change on function of subsonic diffuser

N-area function of supersonic nozzle.

Supersonic diffuser

Laval nozzle

Figure 16 shows two non-design conditions of the supersonic diffuser, denoted by a, b (index n denotes the design condition), with V_ia<V_in<V_ib>a. For each case, the backpressure is also varied so that the subsonic section of the diffuser does not produce a shock wave. In the case of case-a, the convergent section of the diffuser is not able to accommodate such a large amount of gas (it will put up a lot of resistance), so a normal shock wave will be generated before the diffuser, which will increase the pressure to supercritical and reduce the velocity to subsonic. This will cause the convergent part of the diffuser to act as a nozzle. The divergent section of the diffuser will function as a Laval nozzle in the non-design condition.

KeywordsFLOW OF GASES AND STEAM THROUGH DIFFUSERS

5.12

16: Effect of inlet velocity change on supersonic diffuser function

Supersonic diffuser

Throat

The ability to change the back pressure or control the flow area is a prerequisite for the operation of a supersonic diffuser over a wide range of input parameters. The mechanism to control the flow area is not used up to the inlet velocity of about M<1,5 Mach - only the diffuser throat with a constant cross-section is in front of the diverging section of such a diffuser, similar to the one shown in Figure 11. In this design, it is assumed that a normal shock wave is generated at the inlet of the throat, in which the velocity is reduced to subsonic [Dejč, 1967, p. 406]. The losses in such a throat will, at these velocities, still not be significant. More demanding experiments with variable backpressure diffusers, in which shock waves are deliberately generated, are given in [Dejč, 1967, pp. 410-415].

Diffuser profile cascades

Cornut diffuser

Cross pressure gradient

Figure 17 shows that the diffuser profile cascades will have similar characteristics to the cornut diffusers. However, converting the shape of a diffuser profile cascade to an equivalent symmetrical diffuser is problematic. The simple geometric conversion of Figure 17 may not, in terms of flow properties, always be sufficiently predictive. In addition, the sensitivity to boundary layer separation is increased by the cross pressure gradient that arises in the curved channels, hence the low curvature of the profiles in the diffuser cascades.

KeywordsFLOW OF GASES AND STEAM THROUGH DIFFUSERS

5.13

17: Geometric similarity of diffuser blade cascade with symmetrical diffuser

λ-shock wave

If the inlet velocity at the inlet to the diffuser profile grille reaches or exceeds the critical Mach number^3., then the flow exceeds the speed of sound on the suction side of the profile. However, at the outlet of the diffuser channel the pressure is higher than at the inlet, and so is the flow area, so according to Hugoniot's theorem there must be a abrupt change from supersonic to subsonic velocity, this happens locally near the profile in a λ-shock wave^3., see Figure 18. A measure to reduce the effect of such a shock wave is described in [Kadrnožka, 2004, p. 136].

18: Formation of a λ-shock wave in compressor profile cascade

Supersonic compressor

Supersonic profile cascades are rarely used due to their low efficiency and poor controlled operation. Their use is justified, for example, in single-stage compressors with very high compression ratios, see Figure 19.

19: Example of supersonic turbocompressor arrangement

1-radial compressor impeller; 2-diffuser blades with supersonic profile.

KeywordsFLOW OF GASES AND STEAM THROUGH DIFFUSERS

5.14

Ejectors and injectors

Jet machine

Ejectors and injectors are jet machines that are used as vacuum pumps or pumps. The function of ejectors or injectors is based on transferring part of the kinetic energy of the driving fluid to the fluid being driven. This happens approximately at the neck of the diffuser, see Figure 20, where the driven fluid is drawn into the jet of the driving fluid. In the diffuser section of the machine, kinetic energy is transformed into pressure energy.

20: General diagram of ejector or injector

A-driving fluid; B-driven fluid; 1-inlet zone; 2-diffuser neck (mixing zone); 3-outlet diffuser.

Ejector vs. injector

The difference between an ejector and an injector is that the pressure at the outlet of the ejector is lower than the pressure of the driving fluid at the inlet. In contrast, the pressure at the outlet of the injector is higher than the pressure of the driving fluid.

Throat

The shape of the diffuser neck must be designed to gradually transfer the kinetic energy to the driven fluid and balance the velocity field. There must also already be a transformation of kinetic energy into pressure energy in the diffuser neck [Dejč, 1967, p. 416], this contributes to the stabilization of the velocity field and at the same time reduces the internal friction in the diffuser, which is a function of the flow velocity. Thus, the pressure at the inlet of the diffuser must be greater than the pressure at the inlet of the driven fluid.

Ejection ratio

The ratio between the mass flow of the driven and driving fluid, referred to as the ejection ratio, can be determined from the energy balance of mixing in the diffuser neck, see Equation 21.

21: Energy balance of ejectors and injectors

u [J·kg^-1] internal thermal energy of 1 kg working fluid; μ [1] ejection ratio [Dejč, 1967, p. 419]. The derivation of the equation neglecting the effect of the potential energy change is given in Appendix 5. The calculation of the ejector and injector is also carried out in [Hibš, 1981], [Dejč, 1967], [Kadrnožka, 1984], [Nechleba and Hušek, 1966].

KeywordsFLOW OF GASES AND STEAM THROUGH DIFFUSERS

5.15

Internal thermal energy

The internal thermal energy in a jet pump is increased due to losses (kinetic energy or pressure transformation to thermal energy) or heat sharing between the driving and driven fluid. The greatest change in internal thermal energy occurs when one of the working fluids condenses in the neck space. A typical example is the jet feed pump of a steam boiler, see Problem 3.

Ejectors

Mining pump

Vacuum cleaner

Ejectors are widely used in industry, in the mining industry they are used for pumping liquids from great depths [Nechleba and Hušek, 1966, p. 218], in the power industry for suction of steam-air mixture from the condenser of steam turbines where the driving fluid is steam (Figure 22).

22: Example of steam ejector in function as a steam condenser vacuum cleaner [Nožička, 2000]

Injector

Fluid-dynamic pump

Injectors are used as feed water pumps for steam boilers of steam locomotives. The water is pumped to higher pressure using the steam injector, which has an inlet pressure lower than the outlet pressure of the diffuser p_e. This is possible because of the very high kinetic energy the steam can gain in the nozzle during expansion, see Problem 3. The steam transfers this kinetic energy to the water in the mixing chamber (neck of diffuser) and condenses at the same time. A necessary condition for the operation of such a pump is that the vapour still condenses in the neck of the diffuser, or that only liquid without vapour bubbles flows through the diffuser, otherwise the required pressure cannot be achieved. The driving vapour will completely condense in the diffuser neck if an adequate amount of cold water is added. This means that the pump performance decreases with the temperature of the intake water.

Problems

Problem 1:

Cone diffuser

Pressure gradient

Calculate the angle of a conical diffuser and determine the pressure gradient across this diffuser if it has a length of 100 mm and initial radius of 20 mm. Inlet parameters of the diffuser: 82 m·s^-1, 110 kPa, 20 °C, dry air. Outlet parameters: 114 kPa. Consider a lossless flow. The solution to the problem is given in Appendix 1.

KeywordsFLOW OF GASES AND STEAM THROUGH DIFFUSERS

5.16

Figure for Problem 1: grad p [kPa·m^-1] pressure gradient; x [mm].

§1:

entry:

l; r_i; V_i; p_i; t_i; p_e

§3:

calculation:

v_i; v_e; A_i; ε_e; V_e; A_e; r_e; α

§2:

read off:

r; κ

§4:

calculation:

grad p

The procedure for solving Problem 1. Symbol descriptions are in Appendix 1.

Problem 2:

Design a cornut diffuser of circular cross-section corresponding to the requirement dp/dx=const. Diffuser inlet parameters: 82 m·s^-1, 110 kPa, 20 °C, dry air. Diffuser outlet parameters: 114 kPa. The required diffuser length is 100 mm with inlet radius of 20 mm. Consider diffuser efficiency of 93 % with uniformly distributed losses. The solution to the problem is given in Appendix 2.

Calculated radius of diffuser with constant pressure gradient - so-called cornut shape [Frass, 1989, p. 156]. r [mm]; x [mm].

§1:

entry:

V_i; p_i; t_i; p_e; l; r_i; η

§3:

read off:

air states for each p_x from h-s

§2:

calculation:

p_x for each x

§4:

calculation:

r_x for each x

The procedure for solving Problem 2. Symbol descriptions are in Appendix 2.

Problem 3:

Design the basic dimensions of the fluid-dynamic pump steam boiler. The feed water is pumped from an open tank at 70 °C to a pressure of 0,54 MPa. The required feed water flow rate is 60 kg·h^-1. The efficiency of the diffuser section is considered to be 80 %. The nozzle efficiency value includes the efficiency of transfer of kinetic energy from the steam to the pumped water and is 10 %. The saturation steam speed at the pump inlet is 20 m·s^-1. The speed of the water at the inlet and outlet of the pump is 3 m·s^-1. Do not consider pressure losses in the boiler and in the piping. The solution to the problem is given in Appendix 3.

η_A-2 [1] expansion efficiency in nozzle and momentum transfer in mixing chamber (derivation in Appendix 3, §4).

§1:

entry:

p_B; t_B; p₃; m_B; η_2-3; η_A-2; V_A;
V₃; V_B

§5:

read off:

ρ3

§2:

read off:

h_A; s_A; h_B; ρ_B; p_1is; h_1is; ρ_1is

§6:

compare:

ρ3 §5 vs. ρ3 §3

§3:

estimate:

ρ3

§7:

proposal:

V₂; α

§4:

calculation:

μ; h₃

§8:

calculation:

m; A₃; A₂; r₃; r₂; l

The procedure for solving Problem 3. Symbol descriptions are in Appendix 3.

References

ŠKORPÍK, Jiří, 2023, Technická matematika, Transformační technologie, Brno, [online], ISSN 1804-8293. Dostupné z https://engineering-sciences.education/technicka-matematika.html.

ŠKORPÍK, Jiří, 2024, Technická termomechanika, Transformační technologie, Brno, [on-line], ISSN 1804-8293. Dostupné z https://engineering-sciences.education/technicka-termomechanika.html.

KeywordsFLOW OF GASES AND STEAM THROUGH DIFFUSERS

5.17

DEJČ, Michail, 1967, Technická dynamika plynů, SNTL, Praha.

FRAAS, Arthur, 1989, Heat exchanger design, John Wiley&Sons, Inc., ISBN 0-471-62868-9.

GOROŠČENKO, B. T., 1952, Aerodynamika rychlých letounů, Technicko-vědecké vydavatelství, Praha.

HIBŠ, Miroslav, 1981, Proudové přístroje, SNTL – Nakladatelství technické literatury, n. p., Praha, DT 621.694.

JAPIKSE, David, BAINES, N., 1995, Diffuser design technology, Concepts ETI, Norwich, ISBN 0933283083.

KADRNOŽKA, Jaroslav, 1984, Tepelné elektrárny a teplárny, SNTL-Nakladatelství technické literatury, Praha.

KADRNOŽKA, Jaroslav, 2004, Tepelné turbíny a turbokompresory I, Akademické nakladatelství CERM, s.r.o., Brno, ISBN 80-7204-346-3.

MAŠTOVSKÝ, Otakar, 1964, Hydromechanika, Statní nakladatelství technické literatury, Praha.

MICHELE, F. et al., 2010, Historie a současnost Parní turbíny v Brně, Siemens, Brno, ISBN: 978-80-902681-3-5.

NECHLEBA, Miroslav, HUŠEK, Josef, 1966, Hydraulické stroje, Státní nakladatelství technické literatury, Praha.

NOŽIČKA, Jiří, 2000, Osudy a proměny trysky Lavalovy, Bulletin asociace strojních inženýrů, č. 23, ASI, Praha.