MACH NUMBER AND HIGH VELOCITY FLOW EFFECTS

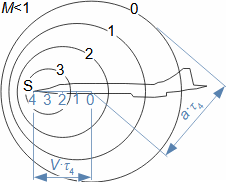
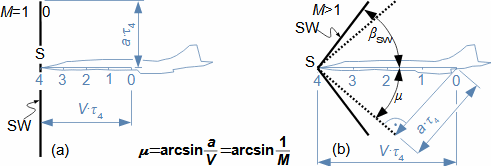
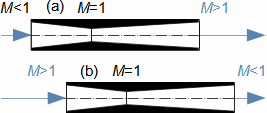
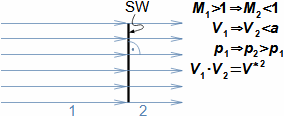
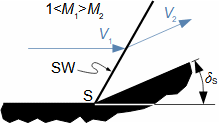
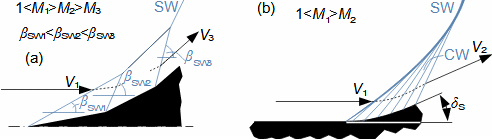
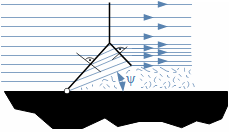
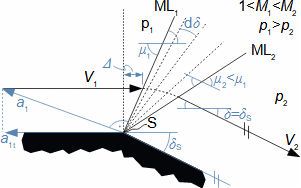
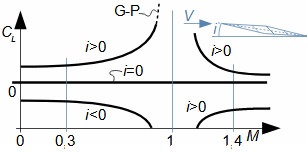
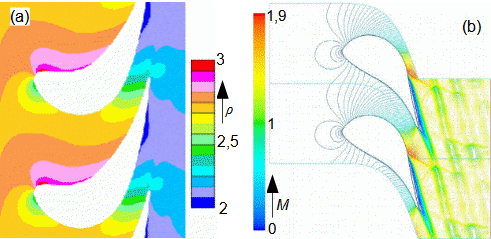
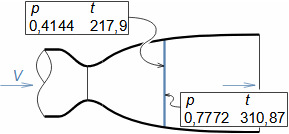
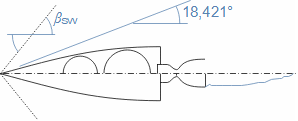
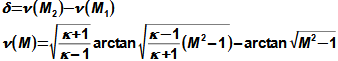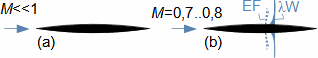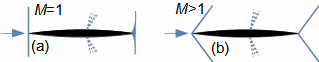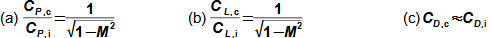Basic concepts in high velocity flow

Mach number

Speed of sound

Compressible fliud

Mach number is defined as the ratio of the velocity of a flow to the velocity of propagation of sound in a fluid (speed of sound), see Equation 1. If the Mach number reaches a value at which the fluid can no longer be considered incompressible for a given application, then such a velocity is considered high in aerodynamics. This is because compressibility causes effects in the flow that do not occur in the flow of incompressible fluids or low Mach numbers. 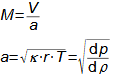It is the general effects of the properties of compressible fluids in flow that are the subject of this article.

1: Definition of Mach number and speed of sound

a [m·s^-1] speed of sound in continuum under investigation; M [Mach] Mach number; p [Pa] pressure; r [J·kg^-1·K^-1] specific gas constant; T [K] absolute gas temperature (static temperature); V [m·s^-1] velocity of body or flow; ρ [kg·m^-3] density; κ [1] heat capacity ratio. The derivation of the equation for the speed of sound is given in Appendix 3.

Subsonic flow

Transonic flow

Sonic flow

Supersonic flow

If the Mach number is less than one (M<1) in the surroundings of the fluid point under investigation, then we speak of subsonic flows. If the value of Mach number in the surroundings of the fluid point under investigation is around 1, specifically in the range 0,8<M<1,3, then we speak of transonic flow - specifically when the Mach number is exactly 1 (M=1) we speak of sonic flow. If the value of Mach number is above 1 (M>1) in the whole surroundings of the fluid point under investigation, then we speak of supersonic flow.

Critical Mach number

Sometimes we come across the term critical Mach number, this number is related to some well-defined point within the fluid volume under investigation, and it is the Mach number at which the speed of sound or supersonic velocity is reached somewhere in the volume (for example, when the fluid is flowing around some bodies inside).

3: Propagation of sound waves when pressure disturbance source moves

τ [s] time. The circles 0, 1, 2, 3 represent the boundary of sound waves in the environment at time τ=0...3. At time 0 the source is just at coordinate 0 at time 1 at coordinate 1 etc. This means that at point 0 the source will cause a pressure disturbance that propagates at the speed of sound in the spherical plane, after the source travels the distance 0-R it will have the radius of the sound wave indicated by the symbol 0 in the figure. The same procedure applies to the pressure disturbance induced by the source at point 1, etc.

Pressure disturbance in supersonic flow

Shock waves

If the source velocity approaches or exceeds the speed of sound in the compressible medium, discontinuities (abrupt state variable changes) occur. Instead of sound waves, pressure disturbances propagate as shock waves.

Shock wave angle

Mach angle

If the pressure disturbance source moves at or above the speed of sound (M≥1), its front is always at the source. This causes the streamlines to not gradually rise in front of the body being bypassed and the body is forced by its volume to displace the surrounding gas byabruptcompression - the energy to compress the gas in the shock wave is taken from the motion of the body. The gas thus compressed gradually expands away from the body. The boundary between the compressed gas and the surrounding gas is cone-shaped and is called a shock wave (Figure 4). The slope of the shock wave β_SW is always greater than the Mach angle μ - their equality would occur for the case of an infinite body.

4: Relationship between shock wave angle and Mach angle

Critical flow speed

If the decrease in the velocity of the supersonic flow occurs only in the narrowing channel, then the speed of sound can only be achieved at the narrowest point of the channel. If this happens, we say that the flow has reached the critical velocity V* in the channel.

Supersonic nozzle

Supersonic diffuser

The behavior of the supersonic flow is therefore exactly opposite to that of the subsonic flow, which is why the two identical channels in Figure 6 operate quite differently in the subsonic and supersonic inlet flows. If the subsonic flow (Figure 6(a)) enters the channel and increases its velocity up to M=1 at the throat, beyond this cross-section the velocity increases further to a highly supersonic outlet velocity, then the channel shown behaves like a supersonic nozzle^4.. Conversely, the channel shown behaves like a supersonic diffuser^5., if a supersonic flow enters the channel, which decreases its velocity to M=1 at the throat, beyond which the velocity further decreases to the low subsonic velocity, thereby transforming the kinetic energy of the supersonic flow into compressive energy.

6: Examples of effect of inlet velocity on function of variable flow area

(a) supersonic nozzle (CD nozzle^4.); (b) supersonic diffuser.

Shock waves

Machines in which supsonic velocities can occur can realistically only be designed for specific conditions (it can be shown that the ratio of the outlet flow area to the minimum flow area must also be different for different Mach numbers), changing the conditions would require changing the geometry of the machine to meet the requirements of the flow transition from supersonic to subsonic. This is often not possible to meet and the transition is made in the expanding part of the flow tube by the abrupt change in the state variables, i.e. the shock wave, only in this way can the conditions of Hugoniot's theorem be met ("smooth transition" is not possible in such a channel). There are several basic types of shock waves according to the conditions under which they are generated, see the following chapters.

Rankine-Hugoniot equations

The shock wave loss depends solely on gas properties and velocity, as evident from Rankine-Hugoniot equations (Equation 9) and Problem 1 calculation. It's independent of the bypassed body's shape.

9: Rankine-Hugoniot equations

The equations are derived for the stable normal shock wave and ideal gas. The derivation of the equations is done in Appendix 5.

Oblique shock waves

Oblique shock wave

Flow deflection

Before the oblique shock wave, velocity must be supersonic, but afterward, it can be subsonic or supersonic. As the flow traverses the oblique shock wave, its direction is deflected by angle δ (Figure 10). Normal velocity components (V_1n, V_2n) share properties with those passing through a normal shock wave (see Problem 2). The equality of tangential velocity components (V_1t=V_2t) can be proved (e.g., [Kadrnožka, 2004, p. 126-127]).

10: Passage of compressible medium by oblique shock wave

δ [°] velocity deflection post-shock from original direction. The index _n denotes the normal velocity components, the index _t denotes tangential velocity components.

Shock wave angle

Shock wave losses

Sound wave

Additionally, analyzing oblique shock wave properties reveals that when β_SW equals the Mach angle μ, V_1n=a₁ must be true, indicating only the sound wave—following the Mach angle definition. It's also demonstrated that the maximum energy loss (entropy increase) happens when β_SW=90°, making losses in the oblique shock wave less than in a normal shock wave for the same pressure ratio ahead and behind the wave.

Crossed shock waves

In actual supersonic compression, instead of compression waves, crossing oblique shock waves are produced with gradually increasing wave angle (Figure 12). At the point of crossing, the effects of these shock waves, i.e. momentum and pressure, are summed. When several shock waves cross successively, their effect is added further away from the body and the resulting wave has even a smaller angle β_SW than the first wave corresponding to a certain flow velocity.

12: Crossed shock waves

(a) rising surface; (b) formation of compression waves at gradually rising surface [Nožička, 2000]. CW-set of compression waves.

Shock wave division

In aviation, experiments have been carried out to reduce the sound effects caused by shock waves in supersonic flights based on the division of the shock wave into several partial waves (shock wave dilution, see Figure 13). This not only reduces the losses in the shock waves, but most importantly, it maximizes the angle of the resulting shock wave (after all shock waves from the fuselage have met). This is because the larger the angle of the shock wave (preferably 90°), the smaller the sound effect from the wave [Hošek, 1962, p. 60] - which would allow transport aircraft to fly at high speeds even over populated areas.

13: Project Quiet Spike

The project successfully explored the possibility of reducing the intensity of sound effects by using a stepped extension of the aircraft's nose. Here, testing of the telescoping nose of F-15B aircraft [Creech, 2009].

Expansion waves

Formation of expansion waves

If the supersonic flow enters a space with increasing cross section it must expand to the higher velocity as predicted by Hugoniot's theorem. Such supersonic expansion takes the form of expansion waves.

Flow deflection

Increasing cross-sectional area also creates obtuse angles on bodies, like the trailing edge of projectiles, the beginning of fuselage taper, etc., as seen in Figure 16, illustrating a typical supersonic obtuse angle flow. When flying around obtuse angles at supersonic velocity, gas must expand from pressure p₁ to p₂, flow velocity increases from V₁ to V₂, and the gas direction is deflected by angle δ from the original. In the expansion wave, there's a gradual change in state variables with very low losses (isentropic expansion).

16: Supersonic flow near obtuse angle

ML-Mach line; Δ [m] length difference.

Mach wave

Prandtl-Meyer function

The formation of the expansion wave in Figure 16 is initiated by the pressure disturbance at the edge S, which propagates upward with velocity a_1t. The ML₁ boundary at which flow direction starts to change and the gas starts to expand is so-called Mach line or also the first expansion wave. It is obvious that the slope of this line is equal to the Mach angle μ₁. During expansion the Mach number changes and the expansion also changes its character because the Mach angle changes. The expansion stops at the Mach line ML₂ where the flowing gas reaches pressure p₂. The first and last Mach lines form the Mach wedge in which the gas expansion takes place. The value of the angle δ can be determined from the Prandtl-Meyer function ν [Anon., 2010], see Equation 17.

Sound and supersonic flow

Normal shock wave

Oblique shock wave

The λ-shock wave moves with increasing velocity towards the trailing edge of the airfoil. When the flow in front of the airfoil reaches the speed of sound, this wave is generated at the trailing edge and normal shock wave starts to form at the leading edge (Figure 19(a)). At supersonic velocity, the frontal normal shock wave transforms into the oblique shock wave and the same happens at the trailing edge where two oblique shock waves are formed by the collision of two supersonic streams from the suction and pressure sides of the airfoil, see Figure 19(b).

19: Flow around lenticular airfoil by sound and supersonic flow

(a) flow around profile at sound speed in front of airfoil; (b) supersonic flow around profile [Kneubuehl, 2004, p. 78].

Space shuttle

The effects in the above paragraphs are observed as the body moves from take-off to high supersonic speed. Figure 20 displays the Space Shuttle Discovery launch (STS-114, 2005). On the left, the image at 50.87 s after launch (Mach 1.2, aerodynamic drag at max), on the right, at 59.72 s (Mach 1.5, aerodynamic drag decreasing).

20: Compressible flow around space shuttle at launch

Photo source [O’Farrell and Rieckhoff, 2011].

Glauert-Prandtl rule

Lift coefficient

Pressure coefficient

Drag coefficient

Laminar airfoil

The Glauert-Prandtl rule converts aerodynamic quantities from incompressible flow measurements to compressible flow using Equation 21. These equations are valid only up to critical Mach or Reynolds numbers [Abbott and Doenhoff, 1959, p. 256 and pp. 283-287], [Hošek, 1949, p. 52]. Profiles with flows below the critical Reynolds number are termed laminar profiles. These equations align with experimental measurements.

It is evident from the above that thin, slightly curved airfoils are sufficient for higher speeds, as anyone will notice in supersonic fighter aircraft, which are slimmer than subsonic machines.

Airfoils for high velocities

Aerodynamics of flight

In a well-designed airfoil, the occurrence of high velocity effects and their effect on the aerodynamics of flight should be predictable. The rhombic airfoil is a good predictor in this respect. Expansion waves are only generated at the tips of the suction and pressure sides, and λ-shock waves are generated at the trailing edge of the airfoil. Of course, this profile is not suitable for low subsonic velocities, so various compromises of profile shapes are found depending on the velocities for which they are primarily intended, see Figure 24.

24: Profile types suitable for high speeds in compressible flow

(a) transonic airfoil; (b) supersonic (lenticular shape); (c) supersonic (rhombic shape); (d) supersonic (trapezoidal shape); (e) hypersonic.

Point of lift

Point of drag

High velocities also cause a shift of the center of lift, which shifts with a change in Mach number [Hošek, 1949, p. 46, 240], and the magnitude of the lift changes simultaneously, see Figure 22. For this reason, modern airplanes are equipped with devices to change the geometry of the wing or shift the center of gravity, and especially at speeds around the speed of sound, they change the pitch to maintain such angles of attack as to keep the lift at the required magnitude - at very high subsonic speeds it can even be negative [Stever and Haggerty, 1966, Flight, p. 69].

Analytical calculation

A closed-form analytical solution can be found for compressible flow in the profile cascade only for the case of one-dimensional compressible flow in the channel - this is equivalent to the analytical solution of nozzles^4. or diffusers^5.. More accurate results that take into account the spatial nature of the flow can be achieved by numerical modelling using powerful computational hardware and appropriate software, see Figure 26.

Problems

p [MPa]; t [°C].

Shock wave angle