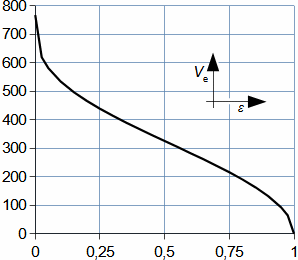
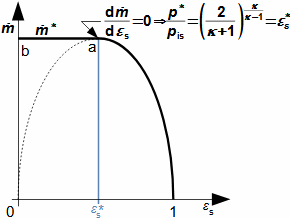
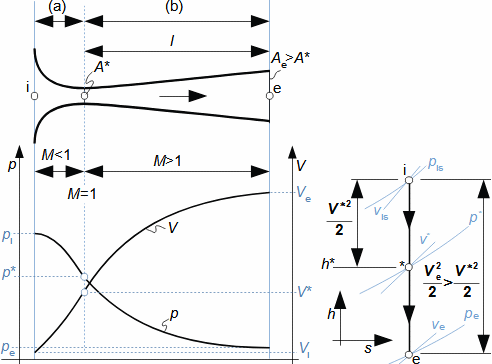
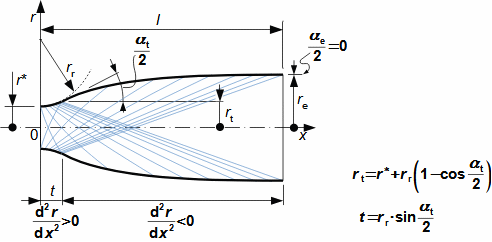
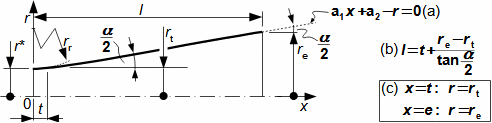
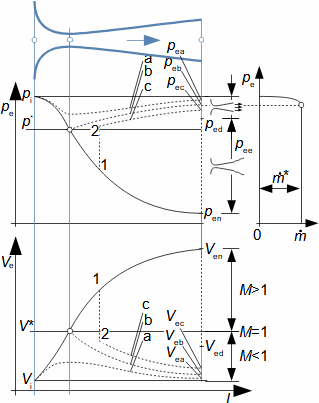
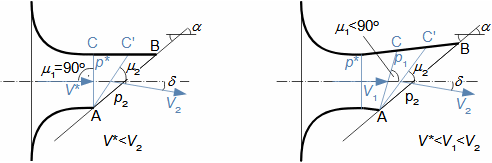
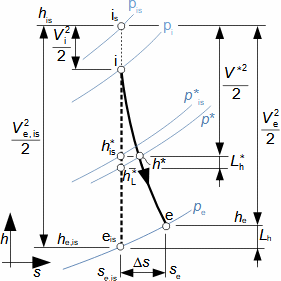
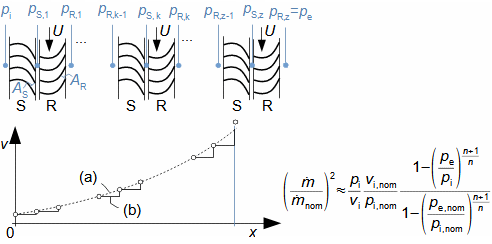
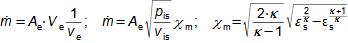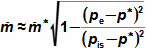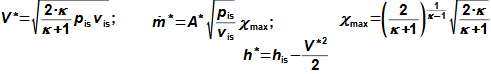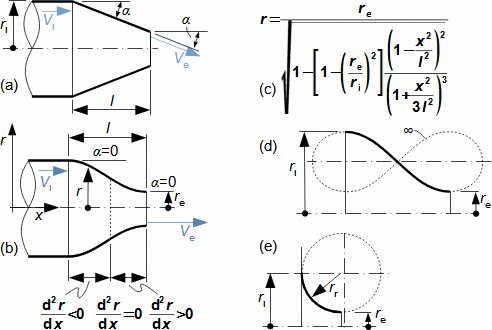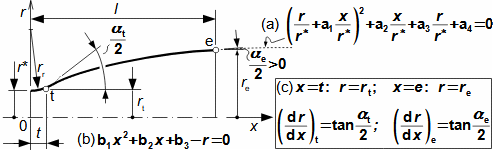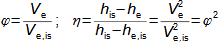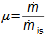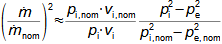Flow of gases and steam through nozzles

Škorpík, Jiří

FLOW OF GASES AND STEAM THROUGH NOZZLES

4.3

What are nozzles and other applications of nozzle theory

What is nozzle?

The nozzle is a channel with a continuously variable flow flow area. Fluid flow in a nozzle is a process in which the pressure decreases and the kinetic energy of the fluid increases.

Convergent nozzle

Convergent-divergent nozzle

The basic nozzle shapes are the convergent or tapering nozzle, in which subsonic expansion takes place, and the convergent-divergent or de Laval nozzle for supersonic expansion, the shape of which is based on Hugoniot's theorem^3. (area-Mach number realation) for the supersonic flow channel.

Nozzle theory

The nozzle theory is well developed and has a wide application in various types of jet machines. In fact, jet theory can be used to describe some apparently complex flows. In addition, a large amount of measured data exists for jets.

Convergent (tapering) nozzle

Expansion in a nozzle is a frequent problem in engineering, which is why the theory of ideal nozzle expansion was developed in the 19th century [Nožička, 2000]. This theory describes the changes of state variables in a nozzle, especially velocity and mass flow. There are several approaches to nozzle shape design, mainly depending on the purpose of the nozzle, the technological complexity of its production and the required maximum length.

Equation for outlet velocity

From the changes of the state variables in the nozzle plotted in the h-s diagram, it can be seen that the gas velocity at the nozzle outlet depends on the inlet pressure p_i and the outlet pressure p_e (back pressure) from the nozzle. Equation 1 for the outlet velocity can then be derived from the First Law of Thermodynamics equation for an open system. This equation is derived for the perfect expansion of an ideal gas without the effect of gravity.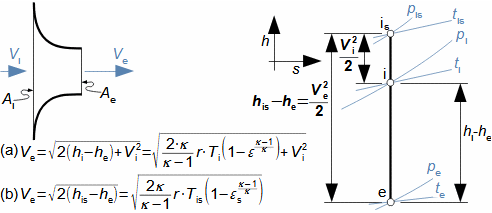

1: Nozzle outlet velocity and pressure ratio

FLOW OF GASES AND STEAM THROUGH NOZZLES

4.4

(a) calculation from the static gas state in front of the nozzle; (b) calculation from the total gas state in front of the nozzle. e-state at the nozzle outlet; i-state at the nozzle inlet. A [m²] flow area of nozzle; h [J·kg^-1] enthalpy; p [Pa] pressure; r [J·kg^-1·K^-1] specific gas constant; s [J·kg^-1·K^-1] entropy; T [K] absolute gas temperature; t [°C] temperature; V [m·s^-1] velocity; ε [1] pressure ratio of static pressures (p_e·p^-1_i); ε_s [1] pressure ratio to stagnation inlet pressure (p_e·p^-1_is); κ [1] heat capacity ratio. The index _s indicates the stagnation state of the gas, the index _i indicates the state at the nozzle inlet, the index _e indicates the state at the nozzle outlet (just inside the nozzle outlet). The derivation of the equation is given in Appendix 6.

Outlet velocity as a function of backpressure

Figure 2 shows the evolution of the gas velocity V_e as the backpressure p_e changes, with the maximum gas velocity at the vacuum outlet being p_e=0.

2: Nozzle outlet gas velocity as function of pressure ratio

p_at [Pa] atmospheric pressure. Gas parameters: κ=1,4, r=287 J·kg^-1·K^-1, t_i=20 °C, p_i=p_at, V_i=0. Chart for ideal gas.

Mass flow through nozzle

The mass flow of gas through the nozzle can be calculated from the continuity equation. In the case of the ideal gas, the ideal gas equation for velocity can be used to obtain an equation for the mass flow through the nozzle as a function of the pressure ratio, see Equation 3.

3: Equation for the mass flow of gas through nozzle

m^• [kg·s^-1] Mass flow through nozzle; v [m³·kg^-1] specific volume; χ_m [1] outlet coefficient. The derivation of the equation for calculating the mass flow through the nozzle is shown in Annex 7.

Outlet coefficient

The outlet coefficient in Equation 3, is based on the fact that for ideal gases only three values of the ideal gas heat capacity ratio κ are considered, see Table 4.

FLOW OF GASES AND STEAM THROUGH NOZZLES

4.5

Critical pressure ratio

The equation for the flow rate, or the outlet coefficient, shows that as the pressure behind the nozzle p_e decreases, the gas mass flow rate m should only increase up to a certain pressure ratio ε_s, then the flow rate should start to decrease, see curve 1-a-0 in Figure 5. In fact, from the ratio ε^*_s until the expansion to vacuum (ε_s=0) the flow rate is constant and equal to m^*, see curve a-b in Figure 5. The pressure ratio at which the maximum gas flow through the nozzle is reached is called the critical pressure ratio (hence the asterisk mark *). The equation for the critical pressure ratio can be derived from the extreme of Equation 3 for the mass flow, see Equation 5.

4: Outlet coefficient values

ε_s	χ_m	χ_m	χ_m	ε_s	χ_m	χ_m	χ_m
	κ=1,3333	κ=1,4	κ=1,6667		κ=1,3333	κ=1,4	κ=1,6667
0,4871	-	-	0,7262	0,76	0,5928	0,5972	0,6115
0,5283	-	0,6847	0,7237	0,78	0,5761	0,5800	0,5925
0,5398	0,6732	0,6845	0,7221	0,8	0,5573	0,5607	0,5715
0,54	0,6732	0,6845	0,7221	0,82	0,5362	0,5391	0,5484
0,56	0,6726	0,6832	0,7184	0,84	0,5125	0,5149	0,5227
0,58	0,6707	0,6807	0,7136	0,86	0,4859	0,4879	0,4942
0,6	0,6676	0,6769	0,7075	0,88	0,4558	0,4573	0,4624
0,62	0,6633	0,6719	0,7002	0,9	0,4214	0,4226	0,4264
0,64	0,6576	0,6656	0,6917	0,92	0,3816	0,3825	0,3852
0,66	0,6506	0,6579	0,6819	0,94	0,3345	0,3351	0,3369
0,68	0,6421	0,6488	0,6708	0,96	0,2764	0,2767	0,2777
0,7	0,6322	0,6383	0,6583	0,98	0,1977	0,1978	0,1982
0,72	0,6208	0,6263	0,6443	1	0	0	0
0,74	0,6077	0,6126	0,6287

χ_m [1], ε_s [1]. For the first three total pressure ratios εs, the flow factors reach their maximum values for a given value of κ.

5: Maximum flow mass through nozzle

The derivation of the critical pressure ratio equation is shown in Annex 8.

FLOW OF GASES AND STEAM THROUGH NOZZLES

4.6

Critical pressure ratio

Hydrogen

Air

Steam

The critical pressure ratio is a function of the gas type because the ratio of heat capacities κ varies from gas to gas. The values of the critical pressure ratios for the ideal gas can be read from Table 4, since it is at these that the values of the outlet coefficient reach their maximum values. The critical pressure ratios of real gases vary slightly, for example, for hydrogen is 0.527, dry air is 0.528, superheated water vapour is 0.546, and saturated water vapour is 0.577. However, the critical pressure ratio can be expected to be around 0.5.

Bendemann ellipse

The 1-a-0 curve of Figure 5 is very close in shape to an ellipse, so in engineering practice, to speed up and simplify nozzle calculations, the 1-a segment is often replaced by a portion of the ellipse called the Bendemann ellipse, see Equation 6, whose validity is limited to the range p_e≥p^*.

6: Bendemann ellipse

The derivation of the equation for the Bendemann ellipse is shown in Appendix 9.

Equation for critical velocity

Nozzle flow cone

At a critical or lower pressure ratio, the flow velocity in the nozzle throat reaches the speed of sound^3., this flow condition is called the critical condition. By substituting the critical pressure ratio (Equation 5) into Equation 1 and Equation 3, equations can be obtained to determine the values of the key quantities for the nozzle throat when the critical pressure ratio is reached or below, see Equation 7. These quantities are called critical (critical velocity, flow rate, pressure ratio, etc.), and in Table 4 the highest values of χ listed are simultaneously the χ_max for a given κ. The graphical representation of the dependence of the flow rate on the inlet pressure and backpressure is called the nozzle flow cone [Škorpík, 2021, p. 42_32].

7: Equations for critical nozzle flow

h* [J·kg^-1] critical enthalpy (in isentropic expansion from the stagnation state, the flow at this enthalpy reaches the critical velocity, or the speed of sound).

FLOW OF GASES AND STEAM THROUGH NOZZLES

4.7

Convergent nozzle shapes

Velocity field

Common convergent nozzle shapes are shown in Figure 8. These shapes can also be applied to non-circular channels and blade passage. The ideal nozzle shape is smooth, parallel to the streamlines (at both inlet and outlet to avoid turbulence due to sudden changes in flow direction against the wall) and one in which a uniform velocity field is achieved at the outlet. That is, the exit velocity should be in the direction of the nozzle axis, as shown by experiments [Dejč, 1967, p. 319]. This condition must also be satisfied by the jet line near the nozzle edge.

8: Effect of nozzle shape on outlet velocity direction

(a) conical nozzle; (b) ideal nozzle shape; (c) Vitoshinsky nozzle [Dejč, 1967, p. 320] (equation holds for l≥2·r_e); (d) the shape of the nozzle as a lemniscate ∞; (e) the shape of the nozzles at the outlet of tanks (r_r≈1,5·r_e [Sutton and Biblarlz, 2010, p. 80]). l [m] nozzle length; r [m] nozzle radius; x [m] nozzle axial coordinate.

Cone nozzle

Lemniscite

Wind tunnel

Cone nozzles are simple to manufacture but have worse flow coefficients (see Flow through nozzle with losses) than nozzles of the shape shown in Figure 8(b). The most uniform velocity field at the outlet is that of Vitoshinsky shaped nozzles (Figure 8(c)) and lemniscate shaped nozzles (Figure 8(d)) - such nozzle shapes are used as a transition channel between two channels and for blowing nozzles in wind tunnels.

FLOW OF GASES AND STEAM THROUGH NOZZLES

4.8

Convergent-divergent nozzle (de Laval nozzle)

If the pressure around the converging nozzle throat is less than the critical pressure, then the critical velocity and critical pressure are set at the nozzle throat so that the gas behind the nozzle continues to expand and its velocity increases to supersonic according to Equation 1. According to Hugoniot's theorem, the flow cross section of the gas stream increases simultaneously. The expanding flow channel creates oblique shock waves^3. at the edges with the surrounding gas, which are reflected inside the flow and reduce the expansion efficiency, see Figure 9. After equilibration of the pressure with the ambient pressure, the expansion ceases and a gradual thermodynamic equilibration of the gas with the ambient gas follows. In order to improve the efficiency of gas expansion beyond the critical nozzle flow area, i.e. for the case p^*>p_e, suitable conditions for the expanding gas must be created, i.e. an expanding channel must be created beyond the narrowest nozzle flow section - such a design is called a convergent-divergent nozzle (de Laval nozzle). There are several shapes of CD nozzles in use, depending on the application and the maximum nozzle length required. However, the length of the nozzle also influences its operating range, as high velocity effects are generated in or around the CD nozzle in a non-design condition.

Nozzle outlet at critical pressure ratio

9: convergent nozzle outlet to pressure lower than the critical pressure

Figure from [Slavík, 1938, s. 5].

Characteristics of CD nozzle

Mach number

The divergent part of the nozzle allows the gas to expand smoothly to supersonic velocities in the nozzle without major losses, see Figure 10, whereby in the convergent part of the nozzle the flow velocity is subsonic M<1, in the divergent part supersonic M>1 and in the throat between them the speed of sound M=1. The h-s diagram of the CD nozzle has the same shape as the h-s diagram of the converging nozzle in Figure 1, and the equation for velocity is the same, except that the gas exceeds the critical parameters during expansion.

FLOW OF GASES AND STEAM THROUGH NOZZLES

4.9

10: CD nozzle - expansion process

(a) convergent part of nozzle; (b) divergent part of nozzle. M [1] Mach number^3.; l [m] length of divergent part of nozzle.

CD nozzle outlet

The discharge velocity of the CD nozzle is supersonic and therefore in free space the flow immediately starts to produce oblique shock waves - braking of the supersonic stream by the surrounding gas, see Figure 11.

11: Supersonic gas outlet from CD nozzle

Figure from [Slavík, 1938, s. 23].

Divergent nozzle shapes

The ideal shape of a CD nozzle is the shape constructed by the so-called characteristic method, but this shape is very demanding to calculate and produce. On the other hand, the simplest shape is the conical nozzle, while bell-shaped nozzles are common in rocketry.

Pohled na konvergentně-divergentní trysky nadzvukového letounu Su-35. Tyto trysky lze navíc otáčet kolem dvou os, což Su-35 umožňuje výbornou manévrovatelnost. pic.twitter.com/rBzuU0cZBt
— Jiří Škorpík (@jiri_skorpik) May 12, 2023

FLOW OF GASES AND STEAM THROUGH NOZZLES

4.10

Method of characteristics

Velocity field

Wind tunnel

Shape of the CD nozzles modelled by the method of characteristics (Figure 12) is the ideal shape. This is because the nozzles designed by this method have a uniform velocity field at the outlet. The method of characteristics is based on the successive construction of expansion waves^3., these waves are plotted in blue in Figure 12. The boundary condition of this method is a given initial radius r_r at α_e=0° (the condition of the outlet velocity in the axial direction) and the flow area at the outlet A_e [Dejč, 1967, p. 341], [Sutton and Biblarlz, 2010, p. 79]. The disadvantage is that the length of such a nozzle is much greater than that of a conical nozzle, so that due to internal friction, its efficiency may be lower than that of a conical nozzle, so this nozzle shape is practically only used where a uniform velocity field at the outlet is very important.

12: Ideal divergent nozzle shape

α [°] diverging nozzle angle; t [m] inlet nozzle length (usually a circular contour with radius r_r≈0,382·r* [Sutton and Biblarlz, 2010, p. 80]). Derivations of the equations for rt and t are shown in Appendix 10.

Cone nozzle equation

Ejector

Injector

The conical CD nozzle is its simplest shape, see Figure 13. This nozzle shape is also used on small rocket engines, small nozzles, single stage heat turbines, on injectors^5. and ejectors^5., etc. The disadvantage of this nozzle shape is that a uniform velocity field cannot be achieved at the outlet, and the deviation of the velocity from the channel axis causes a loss of momentum in the axial direction (about 1 % at an angle α=20° [Sutton and Biblarlz, 2010, p. 78]). The calculation is based on the specified angle α, which is usually 8 to 30°, and the calculated flow area at the outlet A_e. These two parameters are sufficient to calculate the length of the divergent part of the nozzle.

FLOW OF GASES AND STEAM THROUGH NOZZLES

4.11

13: Conical shape of divergent nozzle

(a) equation of nozzle contour; (b) equation for nozzle length; (c) boundary conditions for calculation of the constants a₁, a₂. The derivations of the equations for the calculation of the length of the conical nozzle are shown in Appendix 11.

The bell nozzle equation

The bell nozzle is primarily the shape of rocket engine nozzles. The shape of this nozzle is designed either according to the Rao equation (following G.V.R. Rao, who developed this equation based on experiments [Rao, 1958], [Meerbeeck et al., 2013]) or the Allman-Hoffman equation (following Allman J. G. and Hoffman J. D., who derived the equation by simplifying the Rao equation [Allman and Hoffman, 1981]); both equations are second degree polynomials (parabolas), see Figure 14. In the case of boundary conditions for the Rao equations, the outlet and input angles are interdependent (α_t=f(α_e)). The selection of the optimal pair of input α_t and outlet angle α_e is possible from the length of the equivalent conical nozzle at α=30°, see tables and graphs in [Sutton and Biblarlz, 2010, p. 80]. In the case of the Allman-Hoffman equation, only the input angle α_t is sufficient to solve. A nozzle designed according to the Allaman-Hoffman equation has about 0.2% less exit gas momentum in the axial direction when expanding into vacuum than a nozzle designed according to the Rao equation [Haddad, 1988], but it is easier to work with in finding the optimal nozzle shape for a large number of combinations of working gas input parameters. The bell nozzle is shorter than the conical nozzle, yet has greater efficiency and momentum in the axial direction.

14: Bell nozzle shape

(a) Rao nozzle contour equation; (b) Allman-Hoffman nozzle contour equation; (c) boundary conditions for calculating constants a₁..a₄ or b₁..b₃.

Jestli si dobře pamatuji, tak je to jedna z 10 top knih Elona Muska. https://t.co/kRhd86u21M
— Jiří Škorpík (@jiri_skorpik) March 22, 2022

FLOW OF GASES AND STEAM THROUGH NOZZLES

4.12

Non-design nozzle condition

The discharge pressure p_e,n for which the nozzle is designed is called the design pressure. Thus, the non-design nozzle condition means a condition where the inlet gas parameters or the outlet gas parameters or both parameters are changed. These parameters may change for various reasons (flow control through the nozzle, etc.). In total, there are two basic cases of CD nozzle over-expanded and under-expanded states.

Overexpanded nozzle

If the back pressure p_e is higher than the design pressure p_en, then the nozzle is said to be overexpanded (the nozzle was designed for a "longer" than actual expansion). An overexpanded nozzle can have one of the five possible operating states described in Figure 15, cases a to e, or backpressures p_e,a to p_e,e. Cases c to e are characterized by the generation of normal shock waves^3. according to the back pressure, either in the nozzle, at the nozzle edge (case e), or just behind the nozzle. The occurrence of shock waves at these non-design backpressures can be predicted from Hugoniot's theorem. The shock wave in the nozzle is not stable [Dejč, 1967, p. 363] and can therefore cause vibration of the nozzle and adjacent parts of other machines, and it also significantly increases the noise level. To find the position of the normal shock wave in the nozzle, one can rely on Rankine-Hugoniot equations^3., see Problem 4.

15: CD nozzle - character of flow during back pressure change

Index ₁ indicates the state before the shock wave; index ₂ indicates the state after the shock wave.

FLOW OF GASES AND STEAM THROUGH NOZZLES

4.13

Underexpanded nozzle

If the back pressure p_e is lower than pressure p_en, then the nozzle is said to be underexpanded (the nozzle was designed for a "shorter" expansion than the actual expansion). In cases where the backpressure is lower than the design pressure, the expansion behind the nozzle will continue, similar to a convergent nozzle.

Rocket engine backpressure

Critical nozzle flow area

The change in backpressure also affects the design of rocket engine nozzles. During the rocket's flight in the atmosphere, the external pressure varies with altitude, so the first stage nozzles are designed to expand to atmospheric pressure and the last stage is designed to expand to vacuum [Tomek, 2009]. The greater the thrust range offered by a rocket engine, the more its nozzle must be under-expanded. Therefore, for a perpendicular landing of a rocket with a poorly underexpanded nozzle, the calculation of the ignition of the landing engine must be very precise, because its thrust is de facto constant, so that the rocket acceleration and the engine thrust must be equal just at the contact with the ground.

Motory skycrane, který spustil vozítko Perseverance na povrch Marsu, dokáží regulovat tah v rozsahu 0-100% pomocí škrcení spalin ve spalovací komoře. Něco o těchto motorech a proč je regulace tahu raketového motoru problém:https://t.co/zz3NVbRS2b https://t.co/d9qYWZ4jnk pic.twitter.com/0UxUjdERhf
— Jiří Škorpík (@jiri_skorpik) April 23, 2021

Flow in beveled nozzle

Expansion waves

Prandtl-Meyer function

Mach angle

In a supersonic flow in an beveled nozzle, the flow is deflected from the axial direction due to an expansion wave that originates at the edge of the shorter side of the nozzle, see Figure 16. The situation for an beleved CD nozzle is identical to the flow around an obtuse angle at supersonic speed. The expansion of gas from pressure p₁ starts at line A-C and finishes at line A-C' where pressure p₂ is set. The procedure for calculating the angle δ is given, for example, in [Kadrnožka, 2004, Equations 3.6-10] or Prandtl-Meyer function^3. can also be used.

16: Beleved nozzle - critical flow situation in nozzle throat

right-convergent nozzle; left-convergent-divergent nozzle. α [°] nozzle cutting angle; μ [°] Mach angle^3.; δ [°] jet deflection from nozzle axis.

FLOW OF GASES AND STEAM THROUGH NOZZLES

4.14

Flow through nozzle with losses

If we ignore the non-design states in the nozzle, then the losses that occur in the nozzles are caused by internal friction of the gas. There is also a reduction in flow due to contraction of the flow behind the nozzle throat.

Nozzle friction and vortex losses

Energy dissipation

h-s diagram of nozzle

The internal friction of the gas and the friction against the nozzle walls causes dissipation of energy in the form of frictional heat, which increases the entropy of the gas and thus reduces the resulting kinetic energy of the gas, see Figure 17. In addition, turbulences and vortices can develop in the flow, in which undesirable energy transformations occur on the same principle as in throttling^6., which also leads to an increase in entropy.

17: Flow in nozzle with losses

L_h [J·kg^-1] měrná ztráta v trysce. Index _is označuje stav plynu pro případ izoentropické expanze.

Critical velocity in nozzle during flow with losses

Velocity profile

In a lossy flow, a velocity profile is created in the nozzle so that the velocity of sound will be at the throat in the core of the jet, but near the walls the velocity is subsonic, or the mean kinetic energy of the gas is lower than the corresponding energy at the speed of sound in the entire throat. It is only at a pressure p^* that is lower than p^*_is that the mean kinetic energy of the gas is such that it corresponds to the speed of sound throughout the entire cross section of the gas. Moreover, if at the critical point h^* the gas has different thermokinetic properties from those at h^*_is, then the kinetic energy of the speed of sound will be different from that at isentropic expansion. This means that the enthalpy will also change h*≠h*_is, but these differences between these points are very small.

FLOW OF GASES AND STEAM THROUGH NOZZLES

4.15

Nozzle efficiency

Velocity coefficient

The loss can be calculated from the energy parameters of the nozzle, which are the velocity coefficient φ and the nozzle efficiency η, these two quantities are defined by Formula 18.

18: Nozzle energy parameters

φ [1] velocity coefficient; η [1] nozzle efficiency. The values of the velocity coefficient φ for nozzles are given in [Dejč, 1967, p. 328] for divergent nozzles and in [Dejč, 1967, p. 348] for CD nozzles.

Flow contraction

Vena contracta

The mass flow through the nozzle can be reduced not only due to internal friction in the fluid, but also due to contraction of the flow behind the nozzle throat (vena contracta) [Jarkovsky, 1958 p. 14]. This contraction is due to jet inertia and environmental effects and has the same effect on flow as the reduction in nozzle flow area, see Figure 19. In well-designed nozzles, the contraction of the jet is very small (A_min≈A'_min), whereas it is significant in orifices.

19: Flow contraction in nozzle

A'_min [m²] flow area in the constriction of the stream.

Nozzle flow coefficient

The actual mass flow through the nozzle is calculated using a flow coefficient that includes the effect of internal friction as well as stream contraction. The flow coefficient is defined as the ratio of the actual flow to the flow at isentropic expansion without contraction, see Equation 20. Values of flow coefficients of nozzles and orifices are given in [Dejč, 1967], [Jarkovský, 1958].

20: Flow coefficient

μ [1] flow coefficient; m^•_is [kg·s^-1] flow through nozzle at lossless flow.

FLOW OF GASES AND STEAM THROUGH NOZZLES

4.16

Nozzle as blade passage

Blade passage

Deviation angle

The blade passage can have the shape of a pure convergent nozzle and a convergent-divergent nozzle. Such a blade channel has the characteristics of the beveled nozzle, see Figure 21. CD nozzle blade passages are used where the outlet of the channel must have a supersonic velocity of the working gas - for example, they are used in small single-stage turbines and in the last stages of steam condensing turbines.

21: Situation at outlet of blade row at supersonic flow

(a) confuser blade passage; (b) supersonic blade passage. δ [°] deflection of supersonic flow from the axis of channel, or increase in the deviation angle of the blade row.

Flow through group of nozzles (turbine stages)–Stodola's law

Flow through turbine

Nozzle theory is also used to determine the flow through a group of turbine stages under changed conditions before or after that group of stages. There are several computational procedures (e.g., in [Ambrož, et al., 1956], [Kadrnožka, 1987]), but these have been superseded by numerical calculations. Therefore, we will describe here only the simplest procedure that makes sense to use for approximate calculations, see the application in the article Steam turbine in technological unit [Škorpík, 2011].

Nozzles in series

Blade passage

Turbine stage

The blade passages of a single turbine stage are made up of a stator and a rotor row of blades, with the rotor row located on a shaft that rotates, see Figure 22 and the article Turbomachine – basic concepts [Škorpík, 2021]. The blade passages in these rows can be compared to two nozzles working in series, which means that they are nozzles with the same mass flow. The same assumption can be applied to a group with multistages, or multiple nozzles in series.

Polytropic exponent

specific volume

Two simplifying assumptions are introduced for approximate calculations of the change in flow through a larger group of stages. The first assumption is the adiabatic expansion and its constant value of the polytropic exponent even when the mass flow changes. The second assumption is to simplify the gradual change of the specific volume of gas in the stage to a step change, where the specific volume always changes stepwise at the outlet of the blade passage, see Figure 22.

FLOW OF GASES AND STEAM THROUGH NOZZLES

4.17

22: Formula for approximate calculation of change in flow through large group of turbine stages

(a) evolution of specific volume change in multistage turbine; (b) specific volume change in multistage turbine under the simplifying assumption. R-designation of rotor blade row; S-designation of stator blade row. n [-] exponent of polytropic flow through stage group; x [m] length of stage group under investigation. Indexes: i-state at the entrance to the examined stage group; k-th turbine stage; nom-name state; z-number of turbine stages. The derivation of the equation for the approximate calculation of the change of flow through a large group of turbine stages is given in [Ambrož, et al., 1956, p. 315].

Bendeman ellipse

The general Equation 22 has the disadvantage that it is necessary to look for the root of a polynomial with a general (non-integer) exponent. The solution is to simplify Equation 22 by applying Bendemann's ellipsis to Equation 23. The solution of Equation 23 leads to an easier search for the root of the quadratic equation.

23: Formula for approximate calculation of change in flow through large group of turbine stages derived from Bendemann ellipse

The derivation is given in [Kadrnožka, 1987, s. 181].

Critical pressure ratio

If the critical pressure ratio occurs on the last blade row of a stage group, then the findings for critical nozzle flow can be applied to that stage group. This means that the equation for the flow should be the same as for the vacuum discharge (p_e=0), see Equation 24.

24: Flow through stage group at critical pressure ratio on last blade row

Derived from Equation 23 for vacuum expansion p_e=0.

Stodola's law

The above equations were first derived by Auler Stodola and are therefore referred to as Stodola's law.

FLOW OF GASES AND STEAM THROUGH NOZZLES

4.18

Problems

Problem 1:

Convergent nozzle

Velocity in the nozzle

Mass flow

Air with an initial velocity of 250 m·s^-1, at pressure of 1 MPa and at temperature of 350 °C flows through the nozzle into an ambient pressure of 0.25 MPa. Find (a) whether critical flow occurs, (b) the outlet velocity, (c) the mass floww of air flowing through the nozzle. The outlet flow area of the nozzle is 15 cm². Air properties: C_p=1,01 kJ·kg^-1·K^-1, r=287 J·kg^-1·K^-1, κ=1,4. Do not consider the flow behind the nozzle throat. The solution to the problem is shown in Appendix 1.

Problem 2:

Convergent-divergent nozzle

Design a divergent part of the nozzle (conical shape) to the nozzle designed in Problem 1. Determine the Mach number at the nozzle exit. The angle of the nozzle is 10°. The solution to the problem is shown in Appendix 2.

Problem 3:

Convergent-divergent nozzle

Steam flows through the cone CD nozzle. The pressure and temperature of the steam at the inlet is 80 bar and 500 °C respectively, the pressure at the exit is 10 bar. The nozzle is designed to mass flow 0,3 kg·s^-1. Determine the dimensions of the nozzle. What is the quality of the steam at the exit - superheated/saturated/wet? The angle of the nozzle is α=10°. The solution to the problem is shown in Appendix 3.

Problem 4:

Overexpanded nozzle

Shock wave

Determine the approximate location of the normal shock wave in the CD nozzle from Problem 2 and Problem 1 if the pressure at the nozzle outlet is increased by 0.55 MPa. The solution to the problem is shown in Appendix 4.

x [m] x-axis coordinates.

Problem 5:

Divergent nozzle

Nozzle efficiency

Calculate the dimensions and efficiency of a divergent nozzle of conical shape through which saturated steam flows. The mass flow is 0,2 kg·s^-1. The inlet stagnation pressure is 200 kPa. The back pressure is 20 kPa. The velocity coefficient of the nozzle is 0,95. The solution to the problem is shown in Appendix 5.

References

ŠKORPÍK, Jiří, 2011, Parní turbína v technologickém celku, Transformační technologie, Brno, [on-line], ISSN 1804-8293. Dostupné z https://www.transformacni-technologie.cz/25.html.

ŠKORPÍK, Jiří, 2019, Technická termomechanika, Transformační technologie, Brno, [on-line], ISSN 1804-8293. Dostupné z https://www.transformacni-technologie.cz/43.html.

ŠKORPÍK, Jiří, 2021, Technická matematika, Transformační technologie, Brno, [online], ISSN 1804-8293. Dostupné z https://www.transformacni-technologie.cz/42.html.

ŠKORPÍK, Jiří, 2021, Turbomachine – basic concepts., Transformační technologie,https://www.transformacni-technologie.cz/turbomachine-basic-concepts_112021.html, ISSN 1804-8293.

ALLMAN, J. G., HOFFMAN, J. D., 1981, Design of maximum thrust nozzle contours by direct optimization methods, AIAA journal, Vol. 9, Nb 4, pp. 750-751.

AMBROŽ, Jaroslav, BÉM, Karel, BUDLOVSKÝ, Jaroslav, MÁLEK, Bohuslav, ZAJÍC, Vladimír, 1956 Parní turbíny II, konstrukce, regulace a provoz parních turbín, SNTL, Praha.

DEJČ, Michail, 1967, Technická dynamika plynů, SNTL, Praha.

FLOW OF GASES AND STEAM THROUGH NOZZLES

4.19

HADDAD, A., 1988, Supersonic nozzle design of arbitrary cross-section, Cranfield institute of technology, School of Mechanical Engineering.

JARKOVSKÝ, Eduard, 1958, Základy praktického výpočtu clon, dýz a trubic Venturiho, Státní nakladatelství technické literatury, Praha.

KADRNOŽKA, Jaroslav, 1987, Parní turbíny a kondenzace, VUT v Brně, Brno.

KADRNOŽKA, Jaroslav, 2004, Tepelné turbíny a turbokompresory I, Akademické nakladatelství CERM, s.r.o., Brno, ISBN 80-7204-346-3.

KALČÍK, Josef, SÝKORA, Karel, 1973, Technická termomechanika, Academia, Praha.

MAREŠ, Radim, ŠIFNER, Oldřich, KADRNOŽKA, Jaroslav, 1999, Tabulky vlastností vody a páry, podle průmyslové formulace IAPWS-IF97, VUTIUM, Brno, ISBN 80-2141316-6.

MEERBEECK, W.B.A., ZANDBERGEN, B.T.C., SOUVEREIN, L.J., 2013, A Procedure for Altitude Optimization of Parabolic Nozzle Contours Considering Thrust, Weight and Size, EUCASS 2013 5th European Conference for Aeronautics and Space Sciances, Munich.

NOŽIČKA, Jiří, 2000, Osudy a proměny trysky Lavalovy, Bulletin asociace strojních inženýrů, č. 23, ASI, Praha.

RAO, G. V. R., 1958, Exhaust nozzle contour for optimum thrust, Jet Propulsion, Vol. 28, Nb 6, pp. 377-382.

REKTORYS, Karel, CIPRA, Tomáš, DRÁBEK, Karel, FIEDLER, Miroslav, FUKA, Jaroslav, KEJLA, František, KEPR, Bořivoj, NEČAS, Jindřich, NOŽIČKA, František, PRÁGER, Milan, SEGETH, Karel, SEGETHOVÁ, Jitka, VILHELM, Václav, VITÁSEK, Emil, ZELENKA, Miroslav, 2003, Přehled užité matematiky I, II, Prometheus, spol. s.r.o., Praha, ISBN 80-7196-179-5.

SLAVÍK, Josef, 1938, Modifikace Pitotova přístroje a jeho užití při proudění plynu hubicí, Elektrotechnický svaz Československý, Praha.

SUTTON, George, BIBLARLZ, Oscar, 2010, Rocket propulsion elements, John Wiley& Sons, New Jersey, ISBN: 978-0-470-08024-5.

TOMEK, Petr, 2009, Kde jsou ty (skutečné) kosmické lodě?. VTM Science, vol. 1/2009, Mladá fronta a.s., Praha, ISSN 1214-4754.